《2025年一遍过八年级数学上册华师大版》

1 在△ABC中,若$AC^2 - BC^2 = AB^2,$则 (B)

A.∠A = 90°
B.∠B = 90°
C.∠C = 90°
D.不能确定

答案： B
∵AC² - BC² = AB²,
∴AC² = BC² + AB²,
∴△ABC是以AC为斜边的直角三角形,且∠B=90°.

[2025晋中期末]下列长度的三条线段,能组成直角三角形的是 (C)
A.1,√{2},3
$B.3^2,4^2,5^2$
C.$\frac{5}{4}$,1,$\frac{3}{4}$
D.4,5,6

答案： C
∵1 + √2≈2.414＜3,
∴以1,√2,3为边不能组成三角形,A不符合题意.
∵3²=9,4²=16,5²=25,9² + 16²≠25²,
∴以3²,4²,5²为边不能组成直角三角形,B不符合题意.
∵1² + (3/4)²=(5/4)²,
∴以5/4,1,3/4为边能组成直角三角形,C符合题意.
∵4² + 5²≠6²,
∴以4,5,6为边不能组成直角三角形,D不符合题意.

3 [教材P125练习T2变式]若a,b,c是△ABC的三边长,且$a^2 + (b + c)^2 = 2bc + 2c^2,$则△ABC为 (A)

A.直角三角形
B.锐角三角形
C.钝角三角形
D.等腰直角三角形

答案： A
∵a² + (b + c)²=2bc + 2c²,
∴a² + b²=c²,
∴△ABC为直角三角形,由于条件不足,故D项中的结论无法得到.

4 如图,将△ABC放在网格中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,则∠ABC的度数为 45°。

答案： 45° 由勾股定理,得AC²=1² + 2²=5,BC²=1² + 3²=10,AB²=1² + 2²=5,
∴AB=AC,AC² + AB²=BC²,
∴△ACB是等腰直角三角形,∠BAC=90°,
∴∠ABC=45°.

5 [教材P136习题T4变式][2025洛阳洛龙区期末]在△ABC中,AB = k,AC = k + 1,BC = 3,当k为何值时,∠B = 90°？

答案： 解:
∵∠B=90°,
∴AB² + BC²=AC².
∵AB=k,AC=k + 1,BC=3,
∴k² + 3²=(k + 1)²,解得k=4,
∴当k=4时,∠B=90°.

6 [教材P125例4变式][2025长春东北师大附中月考]已知a,b,c是△ABC的三边长$,a = m^2 - n^2,b = m^2 + n^2,c = 2mn(m ＞ n,m,n$均为正整数). 求证：△ABC是直角三角形.

答案： 证明:
∵m＞n,
∴(m - n)²＞0,即m² - 2mn + n²＞0,
∴m² + n²＞2mn.
∵m² + n²＞m² - n²,
∴m² + n²是最长边.
∵(m² - n²)² + (2mn)²=m⁴ + 2m²n² + n⁴=(m² + n²)²,即a² + c²=b²,
∴△ABC是直角三角形.

7 下列各组数中,是勾股数的是 (C)
A.$\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$
B.2,3,4
C.8,15,17
D.7,24,26

答案： C
∵A选项中的数不是整数,
∴不是勾股数;
∵2² + 3²≠4²,7² + 24²≠26²,
∴B,D选项中的数不是勾股数;
∵8² + 15²=17²,且8,15,17都是正整数,
∴C选项中的数是勾股数.归纳总结勾股数必须是正整数,且以勾股数为长度的线段构成的三角形为直角三角形.

8 [2025新乡期末]观察下列勾股数：3,4,5；5,12,13；7,24,25；….这类勾股数的特点是勾为奇数,弦与股相差为1. 还有一类勾股数,其特点是勾为偶数,弦与股相差为2,例如6,8,10；8,15,17；….若此类勾股数的勾为12,则其弦是 37。

答案： 37 设弦是x,则股为x - 2,则12² + (x - 2)²=x²,解得x=37.

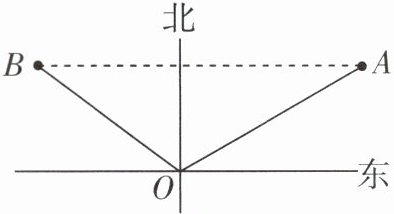
9 [2025天水果积区期末]如图,甲、乙两艘客轮同时离开港口O,航行的速度均为40 m/min,甲客轮用15 min到达A地,乙客轮用20 min到达B地. 若A,B两地的直线距离为1 000 m,甲客轮沿北偏东30°的方向航行,则乙客轮航行的方向是北偏西60°。

答案： 北偏西60° 根据题意,得甲客轮行驶的路程为40×15=600(m),乙客轮行驶的路程为20×40=800(m).
∵600² + 800²=1000²,
∴甲、乙两艘客轮行驶的路线互相垂直,即∠AOB=90°.
∵甲客轮沿北偏东30°方向航行,90° - 30°=60°,
∴乙客轮沿北偏西60°方向航行.

10 [2025梅州期末]如图是某小推车的简化结构示意图,已知BC = 2 dm,CD = 8 dm,AD = 16 dm,AB = 18 dm,其中AD与BD之间是由一个固定为90°的零件连接(即∠ADB = 90°),按照设计要求,需满足BC⊥CD,则该推车符合设计要求吗？并说明理由.

答案： 解:符合.理由如下:
∵AD=16dm,AB=18dm,∠ADB=90°,
∴BD²=AB² - AD²=18² - 16²=68.
∵BC=2dm,CD=8dm,
∴BC² + CD²=2² + 8²=68,
∴BC² + CD²=BD²,
∴BC⊥CD,
∴该推车符合设计要求.