《2025年一遍过八年级数学上册华师大版》

1 阅读以下作图步骤：
①在 $OA$ 和 $OB$ 上分别截取 $OC$,$OD$,使 $OC = OD$；
②分别以点 $C$,$D$ 为圆心,以大于 $\frac{1}{2}CD$ 的长为半径作弧,两弧在 $\angle AOB$ 内交于点 $M$；
③作射线 $OM$,连接 $CM$,$DM$,如图.
根据以上作图,一定可以推得的结论是(A)

A.$\angle 1 = \angle 2$ 且 $CM = DM$
B.$\angle 1 = \angle 3$ 且 $CM = DM$
C.$\angle 1 = \angle 2$ 且 $OD = DM$
D.$\angle 2 = \angle 3$ 且 $OD = DM$

答案： A 由题中作图过程可得,OD=OC,CM=DM;
∵ OM=OM,
∴△COM≌△DOM(SSS),
∴∠1=∠2,
∴A选项符合题意.
∵不能确定OC=CM,OD=DM,OD//CM,
∴∠1=∠3,∠2=∠3不一定成立,故B,C,D选项都不符合题意.

2 如图,在 $\triangle ABC$ 中,根据尺规作图痕迹,下列说法不一定正确的是(B)

A.$AF = BF$
B.$AE = \frac{1}{2}AC$
C.$\angle DBF + \angle DFB = 90^{\circ}$
D.$\angle BAF = \angle EBC$

答案： B 由题图中尺规作图痕迹可知,BE为∠ABC的平分线,直线DF为线段AB的垂直平分线,
∴AF=BF,∠BDF=90°,∠ABF=∠EBC,
∴∠ABF=∠BAF,∠DBF+∠DFB=90°,
∴∠BAF=∠EBC,故选项A,C,D的说法都正确.根据已知条件不能得出AE=$\frac{1}{2}$AC,故选项B的说法不一定正确.

3 如图,在 $\triangle ABC$ 中,$AB = AC$,$CD$ 平分 $\angle ACB$,交 $AB$ 于点 $D$.
(1) 过点 $B$ 作 $BE \perp$ 直线 $CD$ 于点 $E$；(要求：尺规作图,保留作图痕迹,不写作法)
(2) 求证：$\angle ABE + 3\angle ACE = 90^{\circ}$.

答案：
3
(1)解:如图,BE即所求.

(2)证明:
∵CE平分∠ACB,
∴∠BCE=∠ACE.
∵AB=AC,
∴∠ABC=∠ACB=2∠ACE.
∵BE⊥CD,
∴∠BEC=90°,
∴∠ABE=90°-∠BCE-∠ABC=90°-3∠ACE,即∠ABE+3∠ACE=90°.

4 如图,已知 $\triangle ABC$,$\angle A = 60^{\circ}$,$\angle C = 45^{\circ}$.
(1) 在边 $AC$ 上求作一点 $P$,使 $\angle PBC = 45^{\circ}$；
(2) 在 $BP$ 上求作一点 $M$,使得 $AM$ 平分 $\angle BAC$.
(要求：尺规作图,保留作图痕迹,不写作法)

答案：
4 解:
(1)如图,点P即所求.
(2)如图,点M即所求.

5 商朝第一名相、有“烹调之圣”美称的伊尹,晚年曾隐居在连云港市灌云县伊芦山,大小伊山也因他而得名,后人为了纪念他,准备建造一座伊尹雕像. 如图 1,经过实地考察与测量,决定将雕像建造在两条伊尹路内部,并且在两条路所构成的角的平分线上,另外又考虑到让周边 $A$,$B$ 两个小区的人们都方便过来瞻仰,故雕像到 $A$,$B$ 两个小区的距离也相等,请依据上述信息,在图 2 中利用无刻度的直尺和圆规标出伊尹雕像 $P$ 点的位置.(不写作法,保留作图痕迹)

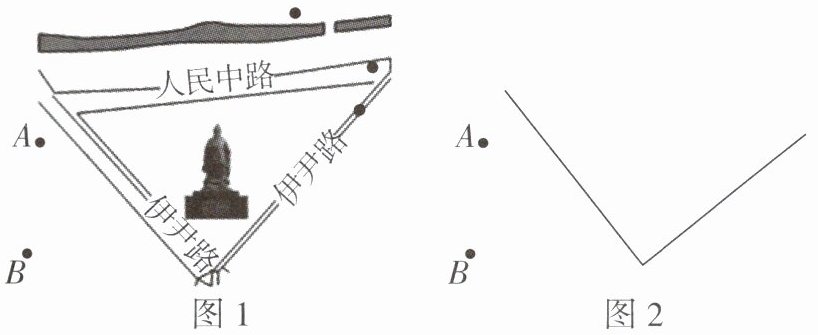
答案：
5 解:如图,点P即所求.