《2025年一遍过八年级数学上册华师大版》

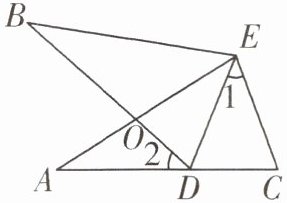
7 如图,$∠A= ∠B,AE= BE$,点 D 在 AC 边上,$∠1= ∠2$,AE 和 BD 相交于点 O. 若$∠C= 71^{\circ }$,则$∠BDE$的度数为(B)

A.$65^{\circ }$
B.$71^{\circ }$
C.$75^{\circ }$
D.$78^{\circ }$

答案： B
∵AE和BD相交于点O,
∴∠AOD=∠BOE.在△AOD和△BOE中,∠A=∠B,∠AOD=∠BOE,
∴∠BEO=∠2.又
∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.在△AEC和△BED中,
∵∠A=∠B,AE=BE,∠AEC=∠BED,
∴△AEC≌△BED(ASA),
∴∠BDE=∠C=71°.

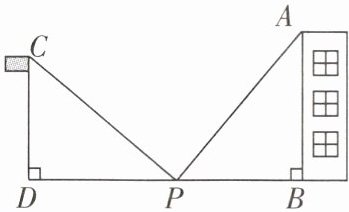
8 [2025 日照期末]八年级的数学兴趣小组开展了测量教学楼的高度的实践活动,方案如下: 如图,①在旗杆 CD 与教学楼 AB 之间选一个点 P;②利用测角仪分别测量旗杆顶点的视线 PC 及教学楼顶的视线 PA 与地面 DB 的夹角$∠CPD= 40^{\circ },∠APB= 50^{\circ }$;③利用卷尺测量点 P 到楼底的距离$PB= 9m$;④利用激光测长仪测量旗杆的高度$CD= 9m$;⑤利用卷尺测量旗杆与教学楼之间的距离$DB= 27m$. 根据数学兴趣小组测量的数据,求教学楼的高度 AB.

答案： 解:根据题意,得CD⊥BD,AB⊥BD,
∴∠CDP=∠PBA=90°,
∴∠DCP+∠CPD=90°.
∵∠CPD=40°,∠BPA=50°,
∴∠CPD+∠BPA=90°,
∴∠DCP=∠BPA.在△CDP和△PBA中,∠DCP=∠BPA,CD=PB,∠CDP=∠PBA,
∴△CDP≌△PBA(ASA),
∴AB=PD=BD - PB=27 - 9=18(m),
∴教学楼的高度AB为18m.

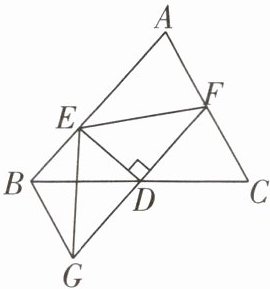
9 如图,在$\triangle ABC$中,D 为 BC 的中点,过点 D 的直线 GF 交 AC 于点 F,交 AC 的平行线 BG 于点 G,$DE⊥GF$于点 D,且交 AB 于点 E,连接 EG,EF.
(1)求证:$BG= CF.$
(2)请你猜想$BE+CF$与 EF 的大小关系,并说明理由.

答案：
(1)证明:
∵BG//AC,
∴∠C=∠GBD.
∵D是BC的中点,
∴BD=DC.在△CFD和△BGD中,∠C=∠GBD,CD=BD,∠CDF=∠BDG,
∴△CFD≌△BGD(ASA),
∴BG=CF.
(2)解:BE+CF＞EF.理由如下:在△BGE中,
∵BE+BG＞EG,
∴BE+CF＞EG.
∵DE⊥GF,
∴∠EDF=∠EDG.由
(1)知△CFD≌△BGD,
∴GD=FD.在△EDF和△EDG中,ED=ED,∠EDF=∠EDG,FD=GD,
∴△EDF≌△EDG(SAS),
∴EF=EG,
∴BE+CF＞EF.

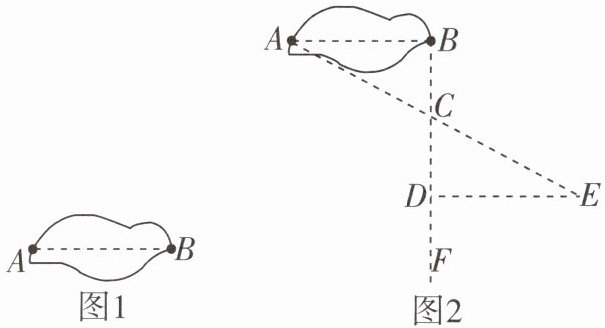
10 教材 P72 例 2 变式模型观念某学校为开展数学实践活动,成立了户外测量小组. 测量小组带有测量工具:绳子、拉尺、小红旗、测角器等. 在学习完数学华东师大版教材八年级上册第 72 页例 2 的题目后,小明小组的同学们准备尝试用不同于例 2 的方法测量某池塘(如图 1)两端 A,B 的距离. 经过思考、讨论,小明小组的同学们最后确定了如下一个测量方法:
如图 2,先过点 B 作 AB 的垂线 BF,再在 BF 上取 C,D 两点,使$BC= CD$,接着过点 D 作 BD 的垂线 DE,交 AC 的延长线于点 E,则测出 DE 的长即该池塘两端 A,B 的距离.
在小明小组的同学们测量方法的基础上,若池塘南面(即点 D,E 附近区域)没有足够空地,点 B 的右侧区域有足够空地并可用于测量.
(1)请你设计一个可行的测量方法,在图1 中画出图形,并进行简单的语言描述.
(2)请对你设计的测量方法进行证明.

答案：

(1)解:测量方法如下:如图,先过点B作AB的垂线BM,在BM上取点D,再由点D观测,在AB的延长线上取一点C,使∠BDC=∠BDA(关键点),此时测出BC的长即该池塘两端A,B的距离.　　　　　　　　　
(2)证明:
∵BD⊥AB,
∴∠ABD=∠CBD=90°.在△ABD和△CBD中,∠ABD=∠CBD,BD=BD,∠BDA=∠BDC,
∴△ABD≌△CBD(ASA),
∴BC=AB.