《2025年一遍过八年级数学上册华师大版》

12 把多项式$x^{2}y^{5} - xy^{n}z$因式分解时,提取的公因式是$xy^{5}$,则$n$的值可能为 (A)
A.6
B.4
C.3
D.2

答案： A 把多项式x²y⁶-xyⁿz因式分解时,提取的公因式是xy⁵,则n≥5.

13 计算$(-2)^{101} + (-2)^{100}$的结果是 (B)
A.$-2$
B.$-2^{100}$
C.2
D.$2^{100}$

答案： B (-2)¹⁰¹+(-2)¹⁰⁰=(-2)¹⁰⁰×(-2+1)=-(-2)¹⁰⁰=-2¹⁰⁰.

14 已知实数$m满足m^{2} - m - 1 = 0$,则$2m^{3} - 3m^{2} - m + 9 = $8.

答案： 8
∵m²-m-1=0,
∴m²-m=1,
∴2m³-3m²-m+9=2m(m²-m)-m²-m+9=2m-m²-m+9=m-m²+9=-(m²-m)+9=-1+9=8.

15 先因式分解,再求值：$(3a - 4b)(7a - 8b) + (11a - 12b)(7a - 8b)$,其中$a = 2$,$b = 1$.

答案： 解:(3a-4b)(7a-8b)+(11a-12b)(7a-8b)=(7a-8b)(3a-4b+11a-12b)=(7a-8b)(14a-16b)=2(7a-8b)(7a-8b)=2(7a-8b)².
当a=2,b=1时,原式=2×(7×2-8×1)²=72.

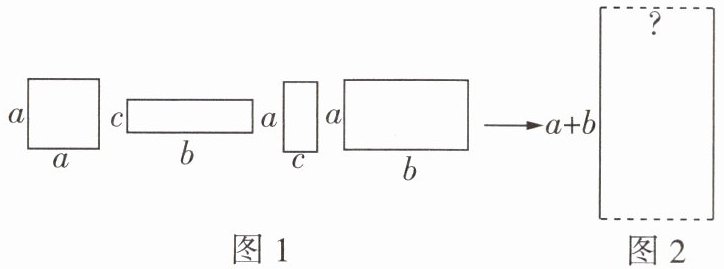
16 图1是甲、乙两个农民伯伯的4块土地的简易图,今年他们决定共同搞投资饲养业,为此他们准备将这4块土地换成一块长为$(a + b)$m的土地(如图2),为使所换到的土地的面积与原来土地的总面积相等,交换后的土地的宽应为多少？

解:
∵原来4块土地的总面积为(a²+bc+ac+ab)m²,a²+bc+ac+ab=a(a+b)+c(a+b)=(a+b)(a+c),且所换到的土地的长为(a+b)m,
∴交换后的土地的宽为(a+c)m.

答案： 解:
∵原来4块土地的总面积为(a²+bc+ac+ab)m²,a²+bc+ac+ab=a(a+b)+c(a+b)=(a+b)(a+c),且所换到的土地的长为(a+b)m,
∴交换后的土地的宽为(a+c)m.

17 [新趋势·代数推理][跨学科·语文]“回文诗”是我国古典文学作品中的特殊体裁,如“遥望四边云接水,碧峰千点数鸿轻”,倒过来便是“轻鸿数点千峰碧,水接云边四望遥”.在数学中也有类似的自然数,称为“回文数”,如11,343等,证明：任意一个四位数的“回文数”$M$一定是11的倍数.

答案： 证明:设任意四位数的“回文数”M的千位,百位,十位和个位上的数字分别为a,b,b,a,则M=1000a+100b+10b+a=1001a+110b=11×91a+11×10b=11(91a+10b),
∴M是11的倍数.

18 [运算能力]先阅读下列因式分解的过程,再回答所提出的问题.
$1 + x + x(x + 1) + x(x + 1)^{2}$
$= (1 + x)[1 + x + x(x + 1)]$
$= (1 + x)^{2}(1 + x)$
$= (1 + x)^{3}$.
(1) 上述分解因式的方法是提公因式法,共应用了2次.
(2) 分解因式：$1 + x + x(x + 1) + x(x + 1)^{2} + x(x + 1)^{3} + x(x + 1)^{4}$.
$1+x+x(x+1)+x(x+1)²+x(x+1)³+x(x+1)⁴=(1+x)[1+x+x(x+1)+x(x+1)²+x(x+1)³]=(1+x)²[1+x+x(x+1)+x(x+1)²]=(1+x)³[1+x+x(x+1)]=(1+x)⁴(1+x)=(1+x)⁵$
(3) 若分解$1 + x + x(x + 1) + x(x + 1)^{2} + … + x(x + 1)^{n}$,则需应用上述方法n次,结果是$(1+x)^{n+1}$.($n$为正整数)

答案： 解:
(1)提公因式法 2
(2)1+x+x(x+1)+x(x+1)²+x(x+1)³+x(x+1)⁴=(1+x)[1+x+x(x+1)+x(x+1)²+x(x+1)³]=(1+x)²[1+x+x(x+1)+x(x+1)²]=(1+x)³[1+x+x(x+1)]=(1+x)⁴(1+x)=(1+x)⁵.
(3)n (1+x)ⁿ⁺¹
1+x+x(x+1)+x(x+1)²+…+x(x+1)ⁿ=(1+x)[1+x+x(x+1)+x(x+1)²+…+x(x+1)ⁿ⁻¹]=(1+x)²[1+x+x(x+1)+x(x+1)²+…+x(x+1)ⁿ⁻²]=…(通过连续提公因式,得出提公因式的次数与结果的指数之间的关系)=(1+x)ⁿ⁺¹.