第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
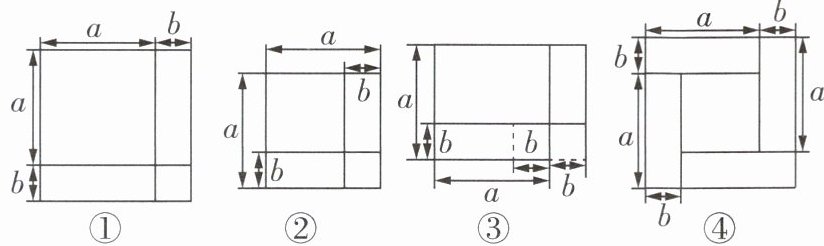
1 [2025 德阳旌阳区期末]我们可以利用图形中的面积关系来解释很多代数恒等式. 给出以下 4 组图形及相应的代数恒等式:①$(a + b)^2 = a^2 + 2ab + b^2$;②$(a - b)^2 = a^2 - 2ab + b^2$;③$(a + b)\cdot (a - b) = a^2 - b^2$;④$(a - b)^2 = (a + b)^2 - 4ab$. 其中,图形的面积关系能正确解释相应的代数恒等式的有 (
A.1 个
B.2 个
C.3 个
D.4 个
D
)
A.1 个
B.2 个
C.3 个
D.4 个
答案:
D
2 我们知道可以用拼图来解释一些多项式的因式分解. 假设有足够多的长方形和正方形卡片,如图 1. 如果选取 1 号、3 号卡片各一张,可以拼成如图 2 所示的形状,根据图 2 可将$a^2 + ab因式分解为a(a + b)$.
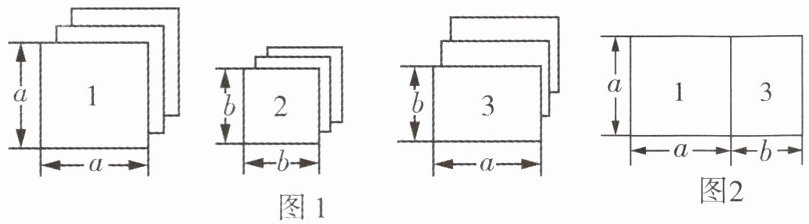
(1)如果分别选取 1 号、2 号、3 号卡片 1 张、1 张、2 张,可拼成如图 3 所示的形状,根据图 3 可将$a^2 + 2ab + b^2$分解因式为______.
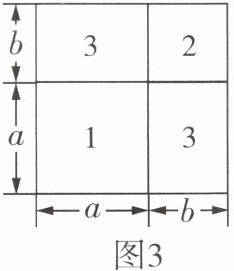
(2)如果分别选取 1 号、2 号、3 号卡片 1 张、2 张、3 张,你能通过拼图形象地说明多项式$a^2 + 3ab + 2b^2$的因式分解吗? 请画出所拼图形,并写出因式分解的结果.
(3)请直接写出$a^2 + 4ab + 3b^2$因式分解的结果.

(1)如果分别选取 1 号、2 号、3 号卡片 1 张、1 张、2 张,可拼成如图 3 所示的形状,根据图 3 可将$a^2 + 2ab + b^2$分解因式为______.

(2)如果分别选取 1 号、2 号、3 号卡片 1 张、2 张、3 张,你能通过拼图形象地说明多项式$a^2 + 3ab + 2b^2$的因式分解吗? 请画出所拼图形,并写出因式分解的结果.
(3)请直接写出$a^2 + 4ab + 3b^2$因式分解的结果.
答案:
解:
(1)$(a+b)^{2}$
(2)能.如图所示(拼图画法不唯一),$a^{2}+3ab+2b^{2}=(a+b)(a+2b).$

(3)$a^{2}+4ab+3b^{2}=(a+b)(a+3b).$
解:
(1)$(a+b)^{2}$
(2)能.如图所示(拼图画法不唯一),$a^{2}+3ab+2b^{2}=(a+b)(a+2b).$

(3)$a^{2}+4ab+3b^{2}=(a+b)(a+3b).$
3 [2025 泉州期末]活动主题:借助图形,直观感受数与形之间的关系.


答案:
解:
(1)$(a+b)^{2}=a^{2}+b^{2}+2ab$
题中图形的面积可以表示为$(a+b)^{2}$,还可以表示为$a^{2}+b^{2}+2ab$,$\therefore (a+b)^{2}=a^{2}+b^{2}+2ab$。
(2)构造的图形如图所示,

$\therefore (a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2ab+2ac+2bc$。
(3)由
(2)可知,$(x+y+z)^{2}=x^{2}+y^{2}+z^{2}+2xy+2xz+2yz$,
$\therefore 2xy+2xz+2yz=(x+y+z)^{2}-(x^{2}+y^{2}+z^{2})$,
$\therefore xy+xz+yz=\frac{1}{2}(x+y+z)^{2}-\frac{1}{2}(x^{2}+y^{2}+z^{2})=\frac{1}{2}m^{2}-\frac{1}{2}n$。
$\because (xy+xz+yz)^{2}=x^{2}y^{2}+x^{2}z^{2}+y^{2}z^{2}+2x^{2}yz+2xy^{2}z+2xyz^{2}$,
$\therefore x^{2}y^{2}+x^{2}z^{2}+y^{2}z^{2}=(xy+yz+xz)^{2}-2xyz(x+y+z)=[\frac{1}{2}(m^{2}-n)]^{2}-2m\cdot (-\frac{1}{4}mn)=\frac{m^{4}+n^{2}}{4}$。
解:
(1)$(a+b)^{2}=a^{2}+b^{2}+2ab$
题中图形的面积可以表示为$(a+b)^{2}$,还可以表示为$a^{2}+b^{2}+2ab$,$\therefore (a+b)^{2}=a^{2}+b^{2}+2ab$。
(2)构造的图形如图所示,

$\therefore (a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2ab+2ac+2bc$。
(3)由
(2)可知,$(x+y+z)^{2}=x^{2}+y^{2}+z^{2}+2xy+2xz+2yz$,
$\therefore 2xy+2xz+2yz=(x+y+z)^{2}-(x^{2}+y^{2}+z^{2})$,
$\therefore xy+xz+yz=\frac{1}{2}(x+y+z)^{2}-\frac{1}{2}(x^{2}+y^{2}+z^{2})=\frac{1}{2}m^{2}-\frac{1}{2}n$。
$\because (xy+xz+yz)^{2}=x^{2}y^{2}+x^{2}z^{2}+y^{2}z^{2}+2x^{2}yz+2xy^{2}z+2xyz^{2}$,
$\therefore x^{2}y^{2}+x^{2}z^{2}+y^{2}z^{2}=(xy+yz+xz)^{2}-2xyz(x+y+z)=[\frac{1}{2}(m^{2}-n)]^{2}-2m\cdot (-\frac{1}{4}mn)=\frac{m^{4}+n^{2}}{4}$。
查看更多完整答案,请扫码查看


