第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1 教材 P116 复习题 T13 变式 [2025 德州期中]如图,在△ABC 和△AED 中,∠C = ∠D,AC = AD,添加下列一个条件后,仍不能证明△ABC ≌ △AED 的是(
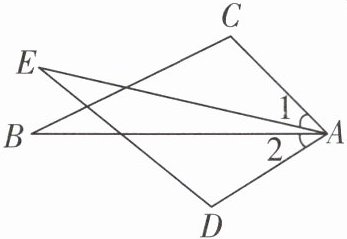
A.∠B = ∠E
B.BC = ED
C.∠1 = ∠2
D.AB = AE
D
)
A.∠B = ∠E
B.BC = ED
C.∠1 = ∠2
D.AB = AE
答案:
D A选项,添加∠B=∠E,可利用“AAS”判定△ABC≌△AED。B选项,添加BC=ED,可利用“SAS”判定△ABC≌△AED。C选项,添加∠1=∠2,
∴∠1+∠EAB=∠2+∠EAB,即∠CAB=∠DAE,可利用“ASA”判定△ABC≌△AED。
∴∠1+∠EAB=∠2+∠EAB,即∠CAB=∠DAE,可利用“ASA”判定△ABC≌△AED。
2 如图,已知△ABC 的六个元素,则甲、乙、丙三个三角形中,和△ABC 全等的是(
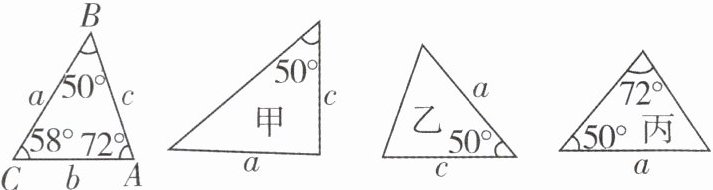
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
B
)
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
答案:
B 在甲中,
∵边长为a,c的边的夹角未知,
∴甲不符合题意;在乙中,两边长分别为a,c,且夹角为50°,符合“SAS”,
∴乙符合题意;在丙中,两角分别是50°,72°,且72°角所对的边长是a,符合“AAS”,
∴丙符合题意。故和△ABC全等的是乙和丙。
∵边长为a,c的边的夹角未知,
∴甲不符合题意;在乙中,两边长分别为a,c,且夹角为50°,符合“SAS”,
∴乙符合题意;在丙中,两角分别是50°,72°,且72°角所对的边长是a,符合“AAS”,
∴丙符合题意。故和△ABC全等的是乙和丙。
3 如图,将长方形纸片 ABCD 沿对角线 BD 折叠,使点 A 落在平面上的点 F 处,DF 与 BC 交于点 E. 求证:△DCE ≌ △BFE.
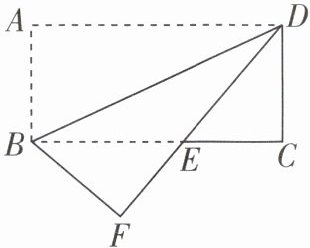

答案:
证明:
∵四边形ABCD为长方形,
∴AB=CD,∠BAD=∠C=90°(长方形的性质)。
根据题意,得BF=AB,∠F=∠A(折叠的性质),
∴DC=BF,∠C=∠F(等量代换)。
在△DCE和△BFE中,
∠C=∠F(已证),∠CED=∠FEB(对顶角相等),DC=BF (已证),
∴△DCE≌△BFE(AAS)。
∵四边形ABCD为长方形,
∴AB=CD,∠BAD=∠C=90°(长方形的性质)。
根据题意,得BF=AB,∠F=∠A(折叠的性质),
∴DC=BF,∠C=∠F(等量代换)。
在△DCE和△BFE中,
∠C=∠F(已证),∠CED=∠FEB(对顶角相等),DC=BF (已证),
∴△DCE≌△BFE(AAS)。
4 [2025 大连期末]如图,在 Rt△ABC 中,∠BAC = 90°,∠ABC 的平分线 BD 交 AC 于点 D,DE ⊥ BC 于点 E. 若△ABC 与△CDE 的周长分别为 15 和 3,求 AB 的长.
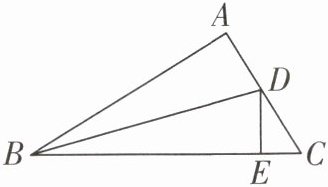

答案:
解:
∵BD平分∠ABC,
∴∠ABD=∠EBD。
∵DE⊥CB,
∴∠DEB=∠A=90°。
在△ABD和△EBD中,
∠A=∠BED,∠ABD=∠EBD,BD=BD,
∴△ABD≌△EBD(AAS),
∴AB=BE,AD=DE,
∴C△ABC - C△DEC=2AB=15 - 3=12,
∴AB=6。
∵BD平分∠ABC,
∴∠ABD=∠EBD。
∵DE⊥CB,
∴∠DEB=∠A=90°。
在△ABD和△EBD中,
∠A=∠BED,∠ABD=∠EBD,BD=BD,
∴△ABD≌△EBD(AAS),
∴AB=BE,AD=DE,
∴C△ABC - C△DEC=2AB=15 - 3=12,
∴AB=6。
5 [2025 广州天河区期中]如图,小明与小敏在玩跷跷板游戏,若跷跷板的支点 O(即跷跷板的中点)到地面的距离是 42 cm,当小敏从水平位置 CD 垂直下降 16 cm 时,求小明离地面的高度.
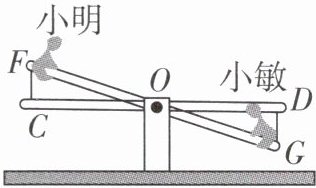

答案:
解:根据题意,
得OF=OG(中点的定义),∠OCF=∠ODG(直角)。
在△OCF和△ODG中,
∠OCF=∠ODG(已证),∠COF=∠DOG(对顶角),OF=OG (已证),
∴△OCF≌△ODG(AAS),
∴CF=DG=16cm(全等三角形的对应边相等),
∴小明离地面的高度为42+16=58(cm)。
得OF=OG(中点的定义),∠OCF=∠ODG(直角)。
在△OCF和△ODG中,
∠OCF=∠ODG(已证),∠COF=∠DOG(对顶角),OF=OG (已证),
∴△OCF≌△ODG(AAS),
∴CF=DG=16cm(全等三角形的对应边相等),
∴小明离地面的高度为42+16=58(cm)。
6 [2025 郑州期末]证明:全等三角形对应边上的中线相等.
在证明几何文字命题时,通常会经历:“画示意图→写已知,求证→写证明过程”这三个步骤. 请按照以上步骤完善下面相应内容.
(1)结合命题的条件和结论,画出符合题意的图形,如下图.
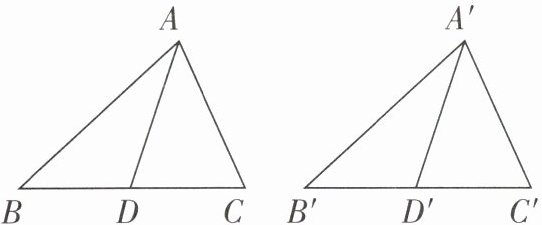
(2)结合(1)中的示意图,请完善已知,求证.
已知:如图,
求证:
(3)写出证明过程.
在证明几何文字命题时,通常会经历:“画示意图→写已知,求证→写证明过程”这三个步骤. 请按照以上步骤完善下面相应内容.
(1)结合命题的条件和结论,画出符合题意的图形,如下图.

(2)结合(1)中的示意图,请完善已知,求证.
已知:如图,
△ABC≌△A'B'C'
,线段 AD,A'D'分别是边 BC,B'C'上的中线.求证:
AD=A'D'
.(3)写出证明过程.
答案:
(2)解:△ABC≌△A'B'C' ,AD=A'D'
(3)证明:
∵△ABC≌△A'B'C',
∴AB=A'B',BC=B'C',∠B=∠B'(全等三角形的对应边相等,对应角相等)。
∵AD,A'D'分别是边BC,B'C'上的中线,
∴BD=1/2BC,B'D'=1/2B'C'(中点的定义),
∴BD=B'D'(等量代换)。
在△ABD和△A'B'D'中,
AB=A'B'(已证),∠B=∠B'(已证),BD=B'D'(已证),
∴△ABD≌△A'B'D'(SAS),
∴AD=A'D'(全等三角形的对应边相等)。
(2)解:△ABC≌△A'B'C' ,AD=A'D'
(3)证明:
∵△ABC≌△A'B'C',
∴AB=A'B',BC=B'C',∠B=∠B'(全等三角形的对应边相等,对应角相等)。
∵AD,A'D'分别是边BC,B'C'上的中线,
∴BD=1/2BC,B'D'=1/2B'C'(中点的定义),
∴BD=B'D'(等量代换)。
在△ABD和△A'B'D'中,
AB=A'B'(已证),∠B=∠B'(已证),BD=B'D'(已证),
∴△ABD≌△A'B'D'(SAS),
∴AD=A'D'(全等三角形的对应边相等)。
查看更多完整答案,请扫码查看


