《2025年一遍过八年级数学上册华师大版》

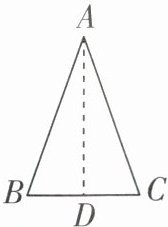
1 在证明“有两个角相等的三角形是等腰三角形”这一判定定理时,慧慧先画出图形,再写出“已知”和“求证”(如下框所示),并给出证明思路：如图,过点$A作BC的垂直平分线AD$,垂足为点$D$。
已知：如图,在$\triangle ABC$中,$\angle B= \angle C$。求证：$AB = AC$。
(1) 慧慧作的辅助线正确吗？若错误,请改正。
(2) 根据慧慧的证明思路,写出完整的证明过程。

答案： 解:
(1)不正确,正确的辅助线作法是过点 A 作AD⊥BC于点 D.
(2)
∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在△ADB和△ADC中,
∠B=∠C,∠ADB=∠ADC,AD=AD,
∴△ADB≌△ADC(AAS),
∴AB=AC(全等三角形的对应边相等).

2 下列能判断$\triangle ABC$为等腰三角形的是(C)
A.$\angle A = 40^{\circ}$,$\angle B = 80^{\circ}$
B.$\angle A = 40^{\circ}$,$\angle B = 60^{\circ}$
C.$\angle A = 20^{\circ}$,$\angle C = 80^{\circ}$
D.$\angle B = 30^{\circ}$,$\angle C = 70^{\circ}$

答案： C

3 [2025 秦皇岛期末]如图,在$\triangle ABC$中,$\angle A = 36^{\circ}$,$\angle C = 72^{\circ}$,折叠该纸片,使点$A$,$B$重合,折痕交$AC于点D$,连接$BD$,则图中的等腰三角形有3个。

答案： 3

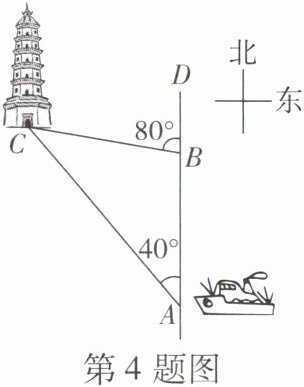
4 [2025 娄底期末]如图,上午$10:00$,一艘轮船从$A地出发以20$海里/时的速度向正北航行,中午$12:00到达B$地,从$A$,$B两地观望灯塔C$,测得$\angle DAC = 40^{\circ}$,$\angle DBC = 80^{\circ}$,则从$B地到灯塔C$的距离为40海里。

答案： 40

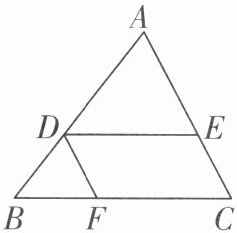
5 [2025 抚州临川一中开学考试]如图,在$\triangle ABC$中,$DE// BC$,$\angle EDF = \angle C$。
(1) 求证：$\angle BDF = \angle A$。
(2) 若$\angle A = 45^{\circ}$,$DF平分\angle BDE$,求$\triangle ABC$的形状。

答案：
(1)证明:
∵DE//BC,
∴∠AED=∠C(两直线平行,同位角相等).
∵∠EDF=∠C,
∴∠EDF=∠AED,
∴DF//AC,
∴∠BDF=∠A(两直线平行,同位角相等).
(2)解:
∵∠BDF=∠A,
∴∠BDF=45°.
∵DF平分∠BDE,
∴∠BDE=2∠BDF=90°.
∵DE//BC,
∴∠B=180° - ∠BDE=90°,
∴∠C=180° - ∠A - ∠B=45°,
∴∠C=∠A,
∴AB=BC(等角对等边),
∴△ABC是等腰直角三角形.

6 给出下列条件：
①三条边都相等的三角形；
②三个内角都相等的三角形；
③一边上的高与中线重合的三角形；
④有一个角为$60^{\circ}$的等腰三角形。
其中能判定该三角形为等边三角形的有①②④。(填序号)

答案： ①②④

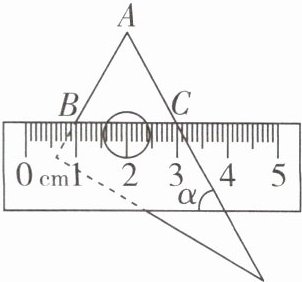
7 [2025 松原宁江区期中]将含$30^{\circ}$角的直角三角尺和直尺按如图所示的方式放置,已知$\angle \alpha = 60^{\circ}$,点$B$,$C表示的刻度分别为1\mathrm{cm}$,$3\mathrm{cm}$,则线段$AB$的长为2$\mathrm{cm}$。

答案： 2