《2025年一遍过八年级数学上册华师大版》

12 小莹在计算 $(◯ - □)^2$ 时,得出的正确结果是 $a^2 - 4ab + (□)^2$,则 $□$ 是 (B)
A.$b$
B.$\pm 2b$
C.$2b$
D.$4b^2$

答案： 12 B

13 [新趋势·过程性学习]已知$ A = (x + 2)^2 + x(1 - x) - 9,$化简 A 时,小明的结果与其他同学的不同,请你检查小明的解题过程(如图所示),他最开始出现错误的是____.(填序号)
$A = (x + 2)^2 + x(1 - x) - 9 = $
$\quad \frac{x^2 + 2x}{①} \frac{+4}{②} \frac{+x - x^2}{③} \frac{-9}{④} = 3x - 5. $
①

答案： 13 ① $A=(x+2)^{2}+x(1-x)-9=x^{2}+4x+4+x-x^{2}-9=5x-5$.

14 [一题多解]设 $M = x + y$,$N = x - y$,$P = xy$. 若 $M = 1$,$N = 2$,则 $P = $$-\frac{3}{4}$.

答案： 14 $-\frac{3}{4}$ 通解 $(x+y)^{2}=x^{2}+2xy+y^{2}=1,(x-y)^{2}=x^{2}-2xy+y^{2}=4$,两式相减,得$4xy=-3$,解得$xy=-\frac{3}{4}$,即$P=-\frac{3}{4}$.优解 由$\left\{\begin{array}{l} M=x+y=1,\\ N=x-y=2,\end{array}\right.$得$\left\{\begin{array}{l} x=\frac{3}{2},\\ y=-\frac{1}{2},\end{array}\right.$$\therefore P=xy=\frac{3}{2}× (-\frac{1}{2})=-\frac{3}{4}$.

15 现有甲、乙、丙三种不同的长方形纸片(边长如图所示).

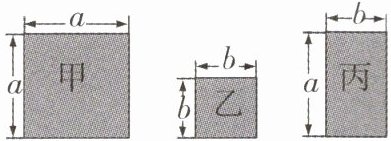
(1) 取甲、乙纸片各 $1$ 块,其面积和为$a^{2}+b^{2}$；
(2) 嘉嘉要用这三种纸片紧密拼接成一个大正方形,先取甲纸片 $1$ 块,再取乙纸片 $4$ 块,还需取丙纸片4块.

答案： 15
(1)$a^{2}+b^{2}$;
(2)4 甲纸片、乙纸片、丙纸片的面积分别为$a^{2},b^{2},ab$.
(1)甲、乙纸片各1块,其面积和为$a^{2}+b^{2}$.
(2)$\because (a+2b)^{2}=a^{2}+4ab+4b^{2}$,$\therefore$用甲纸片1块、乙纸片4块、丙纸片4块,可以拼成一个边长为$a+2b$的正方形.

16 若实数 $m$ 满足 $(m - 2023)^2 + (2024 - m)^2 = 2025$,求 $(m - 2023)(2024 - m)$ 的值.

答案： 16 解:$\because (m-2023)^{2}+(2024-m)^{2}=2025$,$\therefore 2(m-2023)(2024-m)=[(m-2023)+(2024-m)]^{2}-[(m-2023)^{2}+(2024-m)^{2}]=1-2025=-2024$,$\therefore (m-2023)(2024-m)=-1012$.

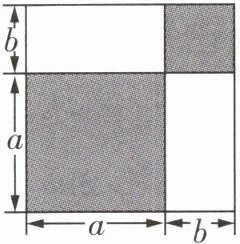
17 [教材 P39 思考变式][2025 新乡期中]观察图形,解答下列问题：
(1) 根据图中的数据,用两种方法表示图中两个阴影图形的面积之和；(只列式,不化简)
(2) 在 (1) 的条件下,你能得到怎样的等量关系？(用等式表示)
(3) 若 $a^2 + b^2 = 53$,$ab = 14$,$a ＞ b ＞ 0$,求 $a + b$ 的值.

答案： 17 解:
(1)方法一:题图中两个阴影图形的面积分别为$a^{2},b^{2}$,$\therefore$两个阴影图形的面积之和为$a^{2}+b^{2}$.方法二:题图中大正方形的面积为$(a+b)^{2}$,空白部分的面积为$ab+ab=2ab$,$\therefore$题图中两个阴影图形的面积之和为$(a+b)^{2}-2ab$.
(2)$a^{2}+b^{2}=(a+b)^{2}-2ab$.
(3)$\because a^{2}+b^{2}=(a+b)^{2}-2ab$,$\therefore a^{2}+b^{2}+2ab=(a+b)^{2}$.$\because a^{2}+b^{2}=53,ab=14$,$\therefore (a+b)^{2}=53+2× 14=81$,$\therefore a+b=\pm 9$.$\because a＞0,b＞0$,$\therefore a+b=9$.

18 小明在计算 $(2a + b - 1)^2$ 时,先将 $(2a + b - 1)^2$ 转化为 $[2a + (b - 1)]^2$,再利用完全平方公式进行计算.
(1) 根据小明的方法计算 $(2a + b - 1)^2$；
(2) 请写出一种与小明不同的转化方式,并写出求解过程.

答案： 18 解:
(1)$(2a+b-1)^{2}=[2a+(b-1)]^{2}$[把$(b-1)$看作一个整体,将三项式转化成可以利用完全平方公式的二项式]$=(2a)^{2}+2\cdot 2a\cdot (b-1)+(b-1)^{2}=4a^{2}+4ab-4a+b^{2}-2b+1$.
(2)不同的转化方式为$[(2a+b)-1]^{2}$.（答案不唯一）$(2a+b-1)^{2}=[(2a+b)-1]^{2}=(2a+b)^{2}-2\cdot (2a+b)\cdot 1+1=(2a)^{2}+2\cdot 2a\cdot b+b^{2}-4a-2b+1=4a^{2}+4ab+b^{2}-4a-2b+1$.

19 [推理能力]若一个正整数等于两个连续奇数的平方差,则称该正整数为“幸福数”. 如：$8 = 3^2 - 1^2$,$16 = 5^2 - 3^2$,故 $8$ 和 $16$ 都是“幸福数”. 下列是“幸福数”的是 (D)
A.$205$
B.$250$
C.$508$
D.$520$

答案： 19 D 若M是“幸福数”,则$M=(2n+1)^{2}-(2n-1)^{2}=8n$($n\geq 1$且n是整数),即“幸福数”能被8整除.$\because$A,B,C选项中的数都不能被8整除,D选项中的数520能被8整除,即$520÷ 8=65$,$\therefore$D选项符合题意.