《2025年一遍过八年级数学上册华师大版》

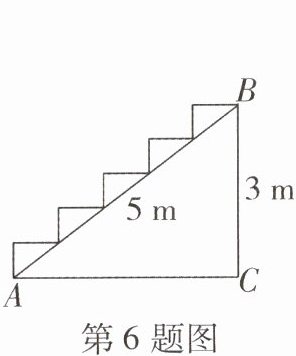
6 [2025 盐城期中] 如图,在高为 3 m,斜坡长为 5 m 的楼梯台阶上铺地毯,则地毯的长度至少为(7m)

A.5 m
B.6 m
C.7 m
D.8 m

答案： C 解题思路:五个台阶的竖直高度是线段BC的长,五个台阶的水平距离是线段AC的长,结合勾股定理即可求解.
在Rt△ABC中,AC=$\sqrt{AB^{2}-BC^{2}}$=$\sqrt{5^{2}-3^{2}}$=4(m),故地毯的长度至少为AC+BC=4+3=7(m).

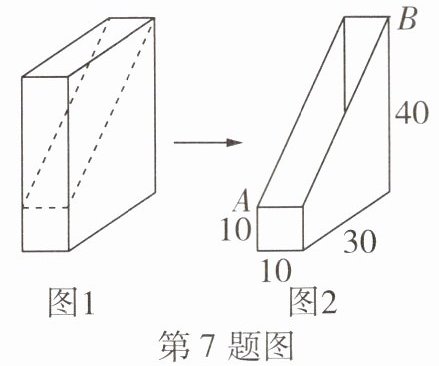
7 新情境 包装纸箱是我们生活中常见的物品. 如图 1,创意 DIY 小组的同学将一个 10 cm×30 cm×40 cm 的长方体纸箱裁去一部分(虚线为裁剪线),得到如图 2 所示的简易书架. 若一只蜘蛛从该书架的顶点 A 出发,沿书架内壁爬行到顶点 B,则它爬行的最短距离为( )

A.50 cm
B.55 cm
C.45 cm
D.60 cm

答案：
A 如图是书架的侧面展开图,连接AB,则AB的长即爬行的最短距离.连接AC,交BD于点O.
∵OA=30+10=40(cm),OB=40 - 10=30(cm),
∴在Rt△AOB中,AB=$\sqrt{OA^{2}+OB^{2}}$=$\sqrt{40^{2}+30^{2}}$=50(cm),
∴蜘蛛爬行的最短距离为50 cm.

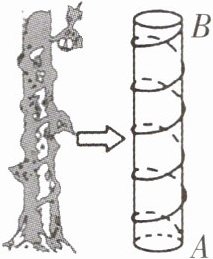
8 新趋势·数学文化 一题多解 [2025 咸阳期中] 我国古代有这样一道数学题：枯木一根直立地上,高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何？题意：如图,把枯木看作一个圆柱体,圆柱的高为 20 尺(一丈是十尺),底面周长为 3 尺,有葛藤自点 A 处缠绕而上,绕五周后其末端恰好到达点 B 处,则问题中葛藤的最短长度是______尺.

答案：
25 通解 如图1,一条直角边AC(即枯木的高)长为20尺,另一条直角边BC长为5×3=15(尺),因此葛藤的最短长度为$\sqrt{20^{2}+15^{2}}$=25(尺).

另解 如图2,将圆柱的侧面展开,则AF=3尺,DF=20÷5=4(尺).
∵AD²=AF²+DF²=3²+4²=5²,
∴AD=5尺,
∴葛藤的最短长度是25尺.

9 [2025 杭州期中] 如图,在一个宽度 EC 为 2 m 的电梯井里,一架 2.5 m 长的梯子 AB 斜靠在竖直的墙 AC 上,顶端 A 被固定在墙上,这时 B 处到墙底端 C 的距离为 0.7 m. 程师傅为方便修理,将梯子的底端举到对面的 D 处,求梯子底端 D 到地面的距离 DE 的长.

答案：
解:如图,过点D作DH⊥AC于点H,
则DH=CE=2 m,DE=CH.
在Rt△ABC中,根据勾股定理得,
AC=$\sqrt{AB^{2}-BC^{2}}$=$\sqrt{2.5^{2}-0.7^{2}}$=2.4(m).
在Rt△ADH中,根据勾股定理得,
AH=$\sqrt{AD^{2}-DH^{2}}$=$\sqrt{2.5^{2}-2^{2}}$=1.5(m),
∴DE=CH=AC - AH=2.4 - 1.5=0.9(m),
∴梯子底端D到地面的距离DE的长为0.9 m.

10 教材 P137 习题 T7 变式 应用意识 如图,A,B 是公路 l(l 为东西走向)同旁的两个村庄,A 村到公路 l 的距离 AC = 2 km,B 村到公路 l 的距离 BD = 4 km,CD = 8 km.
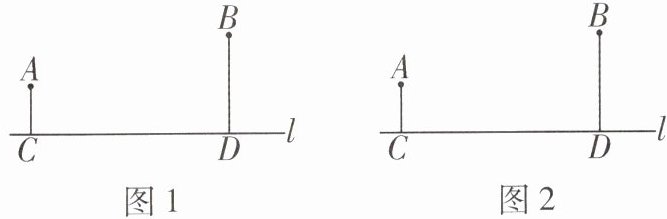
(1)为了方便运输两村的垃圾,现计划在公路边建一个垃圾中转站 M,要求该垃圾中转站到两村的距离之和最小,请用尺规在图 1 中作出点 M 的位置,并求出该最小值；
(2)为方便村民出行,计划在公路边新建一个公共汽车站 P,要求该站到两村的距离相等,请用尺规在图 2 中作出点 P 的位置.(只保留作图痕迹,不写作法)

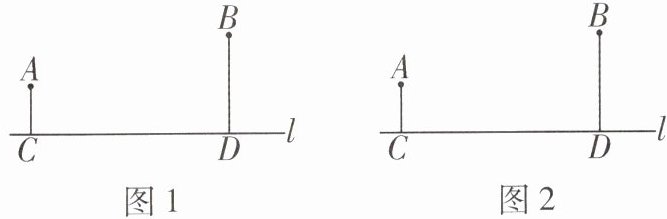
答案：

(1)如图1,作点A关于直线l的对称点A',连接A'B交直线l于点M,连接MA,MB,则点M即所求作的点,此时MA+MB的值最小(“将军饮马”模型).
过点A'作A'F⊥BD,交BD的延长线于点F,
则BF=BD+DF=BD+A'C=BD+AC=4+2=6(km),A'F=CD=8 km.
在Rt△A'BF中,由勾股定理,
得A'B²=8²+6²=100,
∴A'B=10 km,
∴两村距离之和的最小值为10 km.

(2)如图2,连接AB,作线段AB的垂直平分线GH,交直线l于点P,连接PA,PB,则PA=PB,
∴点P即所求.