《2025年一遍过八年级数学上册华师大版》

1 [2025长春期末]下列式子能用平方差公式计算的是(C)
A.$(2a + b)(2b - a)$
B.$(4x + 1)(-4x - 1)$
C.$(2x - y)(y + 2x)$
D.$(x + y)(-y - x)$

答案： C

[2025南通期中]用平方差公式计算$(2x - y + 3)(2x + y - 3)$时,下列变形正确的是(D)
A.$[(2x - y) + 3][(2x + y) - 3]$
B.$[(2x - y) + 3][(2x - y) - 3]$
C.$[2x - (y + 3)][2x + (y - 3)]$
D.$[2x - (y - 3)][2x + (y - 3)]$

答案： D

3 教材P36试一试变式如图(阴影部分面积相等),其中能够验证平方差公式的是①②.(填序号)
]

答案： ①②

4 $(1 + y)(1 - y) = $ (C)

A.$1 + y^{2}$
B.$-1 - y^{2}$
C.$1 - y^{2}$
D.$-1 + y^{2}$

答案： C

5 若$(3b + a)(\quad) = 9b^{2} - a^{2}$,则括号内应填的代数式是(D)
A.$-a - 3b$
B.$a + 3b$
C.$-3b + a$
D.$3b - a$

答案： D

6 若$a + b = 2$,$a - b = 1$,则$a^{2} - b^{2}$的值为2.

答案： 2
∵a+b=2,a-b=1,
∴a²-b²=(a+b)(a-b)=2×1=2.

7 定义$a※b = a(b + 1)$,例如$2※3 = 2×(3 + 1) = 2×4 = 8$,则$(x - 1)※x$的结果为x²-1.

答案： x²-1 根据规定的运算,得(x-1)※x=(x-1)(x+1)=x²-1.

8 [2025上海嘉定区期中]用简便方法计算：$2025^{2} - 2024×2026$.

答案： 解:2025²-2024×2026=2025²-(2025+1)×(2025-1)=2025²-(2025²-1)=2025²-2025²+1=1.

9 [2024济宁中考]先化简,再求值：$x(y - 4x) + (2x + y)(2x - y)$,其中$x = \frac{1}{2}$,$y = 2$.

答案： 解:x(y-4x)+(2x+y)(2x-y)=xy-4x²+4x²-y²=xy-y².当x=$\frac{1}{2}$,y=2时,原式=$\frac{1}{2}$×2-2²=1-4=-3.

10 利用平方差公式计算：
(1)$197×203$；
(2)$40\frac{1}{3}×39\frac{2}{3}$.

答案：
(1)197×203=(200-3)×(200+3)=200²-3²=40000-9=39991；
(2)40$\frac{1}{3}$×39$\frac{2}{3}$=(40+$\frac{1}{3}$)×(40-$\frac{1}{3}$)=40²-($\frac{1}{3}$)²=1600-$\frac{1}{9}$=1599$\frac{8}{9}$.

11 教材P37例3变式[2025十堰实验中学模拟]从前,某人把一块边长为$a\ m(a ＞ 6)$的正方形土地租给租户张老汉.第二年,他对张老汉说：“我把这块地的一边增加$6\ m$,相邻的一边减少$6\ m$,变成长方形土地继续租给你,租金不变,你也没有吃亏,你看如何？”如果这样,张老汉的租地面积(C)

A.没有变化
B.变大了
C.变小了
D.无法确定

答案： C
∵a²-(a+6)(a-6)=a²-a²+36=36＞0,
∴a²＞(a+6)(a-6),
∴张老汉的租地面积变小了.

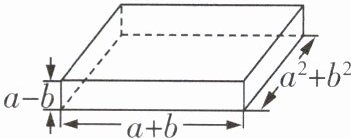
12 求如图所示的长方体的体积.(用含$a$,$b$的代数式表示)
]

答案： 解:(a+b)(a-b)(a²+b²)=(a²-b²)(a²+b²)=a⁴-b⁴.故题图中长方体的体积为a⁴-b⁴.