《2025年一遍过八年级数学上册华师大版》

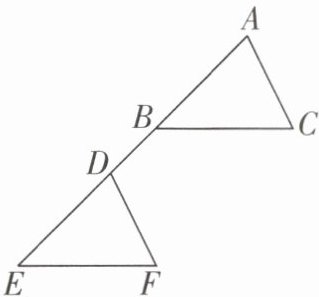
1 [2025 北京昌平区期末]如图,点 A,B,D,E 在同一条直线上,$AD= BE,BC// EF,∠A= ∠EDF$. 求证:$\triangle ABC\cong \triangle DEF$.

答案： 证明:
∵AD=BE,
∴AD - BD=BE - BD,即AB=DE(等式的基本性质1).
∵BC//EF,
∴∠ABC=∠E(两直线平行,同位角相等).在△ABC和△DEF中,∠A=∠EDF(已知),AB=DE(已证),∠ABC=∠E(已证),
∴△ABC≌△DEF(ASA).

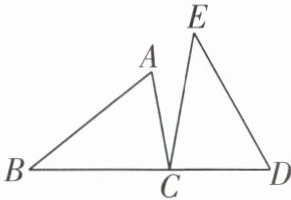
2 [2025 松原宁江区期中]如图,点 C 在线段 BD 上,在$\triangle ABC和\triangle DEC$中,$∠A= ∠D,AB= DE,∠B= ∠E$. 求证:$AC= DC$.

答案： 证明:在△ABC和△DEC中,∠A=∠D(已知),AB=DE(已知),∠B=∠E(已知),
∴△ABC≌△DEC(ASA),
∴AC=DC(全等三角形的对应边相等).

3 新趋势·尺规作图[2025 承德期中]如图是一块缺角的$\triangle ABC$残片,请你利用尺规,作一个和$\triangle ABC$全等的三角形,并写出证明过程.(不写作法,保留作图痕迹)

答案：
解:如图,△FDE即所求.　　 　　 根据作图可得,∠EFD=∠A(已作),FD=AB(已作),∠EDF=∠B(已作)
∴△FDE≌△ABC(ASA).

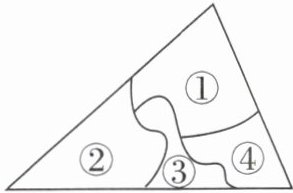
4 教材 P88 习题 T7 变式小华同学周末在家做家务,不慎把家里的一块三角形玻璃打碎成了如图所示的四块,小华要去玻璃店配一块完全一样的玻璃,可以选择(A)

A.带①②去
B.带②③去
C.带③④去
D.带②④去

答案： A 带①②去,符合三角形全等的基本事实“ASA”

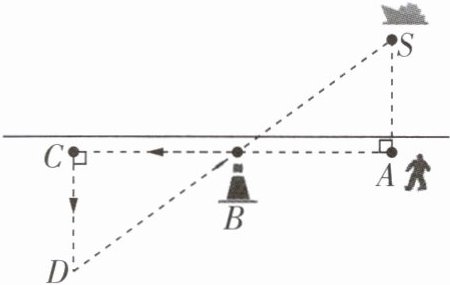
5 北师七下教材 P112 习题 T2 如图,小明站在堤岸的 A 点处,正对他的 S 点处停有一艘游艇. 他想知道这艘游艇距离他有多远,于是他沿堤岸走到电线杆 B 旁,接着再往前走相同的距离,到达 C 点. 然后他向左直行,当看到电线杆与游艇在一条直线上时停下来,此时他位于 D 点. 那么 C,D 两点间的距离就是在 A 点处小明与游艇的距离. 你知道这是为什么吗?

答案： 解:结合题图可知∠A=∠C=90°.
∵小明沿堤岸走到电线杆B旁,接着再往前走相同的距离,到达C点,
∴AB=CB.在△ABS和△CBD中,∠A=∠C=90°,AB=CB,∠ABS=∠CBD,
∴△ABS≌△CBD(ASA),
∴AS=CD,
∴C,D两点间的距离就是在A点处小明与游艇的距离.

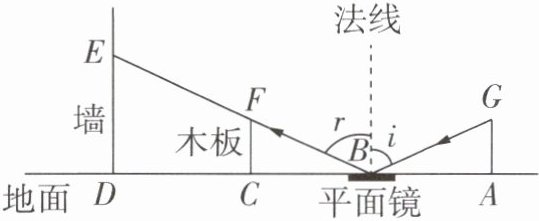
6 跨学科·物理[2025 南阳期末]如图,乐乐用手电筒进行物理光学实验,地面上从左到右依次是墙、木板和平面镜,手电筒的光线从点 G 出发,在平面镜上的 B 处反射后,经过木板的边缘点 F 落在墙上的点 E 处. 已知$FC⊥AD$于点 C,$GA⊥AD$于点 A,点 F 到地面的距离$CF= 1.5m$,点 A,C 到平面镜 B 的距离相等,点 A,B,C,D 在同一条直线上,求手电筒到地面的距离 AG. (注:法线与地面垂直,入射角$i= 反射角r$)

答案： 解:根据题意,得∠i=∠r,
∴90° - ∠i=90° - ∠r,
∴∠ABG=∠CBF(等式的基本性质1).
∵FC⊥AD,GA⊥AD,
∴∠GAB=∠FCB=90°(垂直的定义).在△GAB和△FCB中,∠ABG=∠CBF(已证),AB=CB(已知),∠GAB=∠FCB=90°(已证),
∴△GAB≌△FCB(ASA),
∴AG=CF=1.5m(全等三角形的对应边相等).