第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
8 [2025 赣州期中]如图,等边三角形纸片$ABC的边长为6$,$E$,$F是边BC$上的三等分点,分别过点$E$,$F沿着平行于BA$,$CA$方向各剪一刀,则剪下的$\triangle DEF$的周长是(
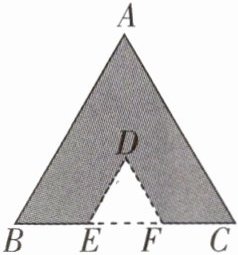
A.$5$
B.$6$
C.$7$
D.$8$
B
)
A.$5$
B.$6$
C.$7$
D.$8$
答案:
B
9 教材$\mathrm{P}99习题\mathrm{T}3$变式 在如图所示的五个三角形中,$AB = AC$,则经过三角形一个顶点的一条直线不能够将这个三角形分成两个小等腰三角形的是
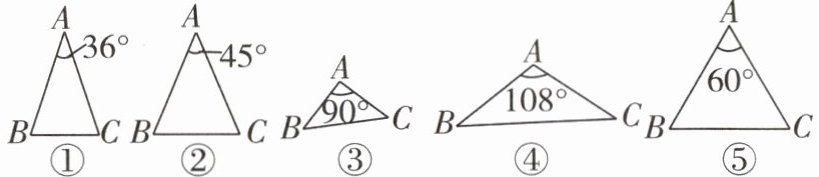
②⑤
。(填序号)
答案:
②⑤
10 如图,$\triangle ABC$是等边三角形,边长为$5$,$\angle ABC和\angle ACB的平分线交于点F$,过点$F作BC的平行线分别交AB$,$AC于点D$,$E$,求$\triangle ADE$的周长。
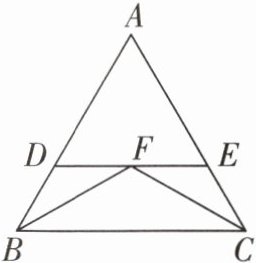

答案:
解:
∵BF平分∠ABC,
∴∠DBF=∠CBF.
∵BC//DE,
∴∠DFB=∠CBF,
∴∠DBF=∠DFB,
∴DF=DB.
同理可得EF=EC,
∴△ADE的周长=AD + DF + EF + AE=AD + BD + CE + AE=AB + AC=5 + 5 = 10.
∵BF平分∠ABC,
∴∠DBF=∠CBF.
∵BC//DE,
∴∠DFB=∠CBF,
∴∠DBF=∠DFB,
∴DF=DB.
同理可得EF=EC,
∴△ADE的周长=AD + DF + EF + AE=AD + BD + CE + AE=AB + AC=5 + 5 = 10.
11 [2025 常德期末]为测量一条两岸平行的河流的宽度,三个数学活动小组设计了三种方案,他们在河流南岸的点$B测得河流北岸的树A在点B$的正北方,测量方案如下:
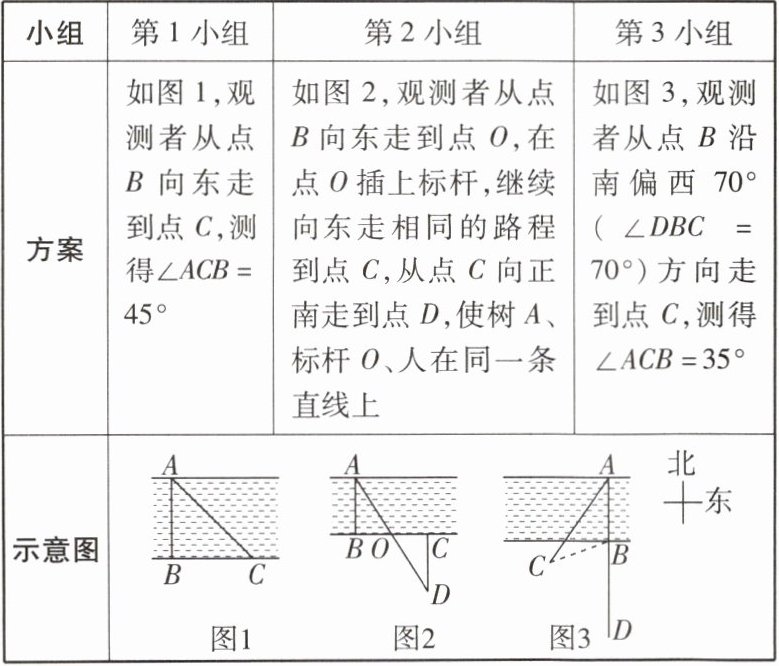
(1) 第$1小组要求河宽AB$,只需测出线段
(2) 第$2小组测得CD = 30\mathrm{m}$,则河宽$AB= $
(3) 第$3小组只要测得BC$的长,就能得到河宽$AB$,你认为第$3$小组的方案可行吗?若可行,请给出证明;若不可行,请说明理由。

(1) 第$1小组要求河宽AB$,只需测出线段
BC
的长。(2) 第$2小组测得CD = 30\mathrm{m}$,则河宽$AB= $
30
$\mathrm{m}$。(3) 第$3小组只要测得BC$的长,就能得到河宽$AB$,你认为第$3$小组的方案可行吗?若可行,请给出证明;若不可行,请说明理由。
答案:
(1)BC
根据题意,得∠ABC=90°.
∵∠ACB=45°,
∴∠BAC=90° - ∠ACB=45°,
∴∠BAC=∠ACB=45°,
∴AB=BC.
(2)30
根据题意,得OB=OC,∠ABO=∠DCO=90°.在△ABO和△DCO中,∠ABO=∠DCO,OB=OC,∠AOB=∠DOC,
∴△ABO≌△DCO(ASA),
∴AB=CD=30 m.
(3)可行.证明如下:
∵∠DBC=70°,∠ACB=35°,
∴∠BAC=∠DBC - ∠ACB=70° - 35° = 35°,
∴∠BAC=∠ACB=35°,
∴AB=BC,
∴只要测得BC的长就能得到河宽AB.
(1)BC
根据题意,得∠ABC=90°.
∵∠ACB=45°,
∴∠BAC=90° - ∠ACB=45°,
∴∠BAC=∠ACB=45°,
∴AB=BC.
(2)30
根据题意,得OB=OC,∠ABO=∠DCO=90°.在△ABO和△DCO中,∠ABO=∠DCO,OB=OC,∠AOB=∠DOC,
∴△ABO≌△DCO(ASA),
∴AB=CD=30 m.
(3)可行.证明如下:
∵∠DBC=70°,∠ACB=35°,
∴∠BAC=∠DBC - ∠ACB=70° - 35° = 35°,
∴∠BAC=∠ACB=35°,
∴AB=BC,
∴只要测得BC的长就能得到河宽AB.
12 教材$\mathrm{P}116复习题\mathrm{T}15$变式 [2025 济宁期末]如图,$B$,$E$,$C$,$F是直线l$上的四点,$AC$,$DE相交于点G$,$AB = DF$,$AC = DE$,$BC = EF$。
(1) 求证:$\triangle GEC$是等腰三角形。
(2) 连接$AD$,求直线$AD与l$的位置关系。
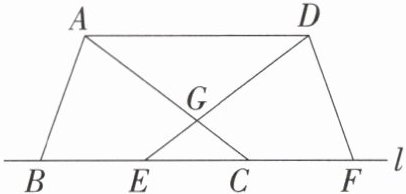
(1) 求证:$\triangle GEC$是等腰三角形。
(2) 连接$AD$,求直线$AD与l$的位置关系。

答案:
(1)证明:在△ABC和△DFE中,
AB=DF,AC=DE,BC=FE,
∴△ABC≌△DFE(SSS),
∴∠ACB=∠DEF,
∴EG=CG,
∴△GEC是等腰三角形.
(2)解:
∵AC=DE,EG=CG,
∴AC - CG=DE - EG,
∴AG=DG,
∴∠GAD=∠GDA=$\frac{1}{2}$(180° - ∠AGD).
∵∠ACE=∠DEF=$\frac{1}{2}$(180° - ∠CGE),∠AGD=∠CGE,
∴∠GAD=∠ACE,即∠CAD=∠ACB,
∴AD//l.
(1)证明:在△ABC和△DFE中,
AB=DF,AC=DE,BC=FE,
∴△ABC≌△DFE(SSS),
∴∠ACB=∠DEF,
∴EG=CG,
∴△GEC是等腰三角形.
(2)解:
∵AC=DE,EG=CG,
∴AC - CG=DE - EG,
∴AG=DG,
∴∠GAD=∠GDA=$\frac{1}{2}$(180° - ∠AGD).
∵∠ACE=∠DEF=$\frac{1}{2}$(180° - ∠CGE),∠AGD=∠CGE,
∴∠GAD=∠ACE,即∠CAD=∠ACB,
∴AD//l.
13 新趋势·尺规作图 教材$\mathrm{P}96练习\mathrm{T}4$变式 [2024 陕西中考$\mathrm{A}$卷]如图,已知直线$l和l外一点A$,请用尺规作图法,求作一个等腰直角三角形$ABC$,使得顶点$B和顶点C都在直线l$上。(作出符合题意的一个等腰直角三角形即可,保留作图痕迹,不写作法)
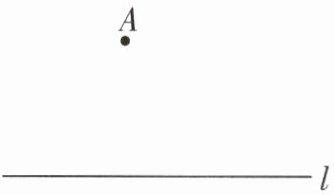

答案:
解:如图1,等腰直角三角形ABC即所求.(或如图2,等腰直角三角形ABC即所求)
查看更多完整答案,请扫码查看


