《2025年一遍过八年级数学上册华师大版》

12 新考法 [2025 镇江京口区期中]王老师把家里的 Wi-Fi 密码设置成数学问题,小明同学来王老师家做客,看到如图所示的 Wi-Fi 密码图片,思索了一会儿,输入密码,顺利地连接上了王老师家的网络,则小明同学输入的 Wi-Fi 密码是yang48888。

答案： yang48888

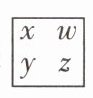
13 [2025 汉中汉台区月考]三角  $\begin{array}{c} \overset{a}{◯} \\ b\quad c \end{array} $ 表示 $3abc$,方框 $\begin{array}{|cc|} \hline x & w \\ \hline y & z \end{array} $ 表示 $-4x^{y}w^{z}$,则 $\begin{array}{c} \overset{m}{◯} \\ n\quad 3 \end{array} × \begin{array}{|cc|} \hline n & m \\ \hline 2 & 5 \end{array} = $-36m⁶n³。

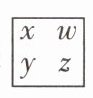
答案： -36m⁶n³

14 [2025 重庆九龙坡区期末]国旗的旗面为红色长方形,其长与宽之比为 $3:2$,有五种通用尺度(尺寸规格)。若一种尺度的国旗的宽为 $b$,求这种尺度的国旗的旗面的面积。

答案： 解:
∵国旗旗面的长与宽之比为3:2,
∴长是宽的$\frac{3}{2}$倍.又
∵国旗的宽为b,
∴长为$\frac{3}{2}$b,
∴这种尺度的国旗的旗面的面积为b·$\frac{3}{2}$b=$\frac{3}{2}$b².

15 已知 $A = 3x^{2}$,$B = -2xy^{2}$,$C = -x^{2}y^{2}$,求 $A\cdot B^{2}\cdot C$ 的值。

答案： 解:A·B²·C=(3x²)·(-2xy²)²·(-x²y²)=3x²·4x²y⁴·(-x²y²)=-12x⁶y⁶.

16 [2025 盐城段考]若 $a^{m + 1}b^{n - 2}\cdot a^{2n - 1}b^{2n} = a^{5}b^{3}$,求 $m + n$ 的值。

答案： 解:
∵a^{m+1}b^{n-2}·a^{2n-1}b^{2n}=a^{m+1+2n-1}·b^{n-2+2n}=a^{m+2n}b^{3n-2}=a⁵b³,
∴$\begin{cases}m+2n=5, \\3n-2=3,\end{cases}$解得$\begin{cases}m=\frac{5}{3}, \\n=\frac{5}{3},\end{cases}$
∴m+n=$\frac{10}{3}$.

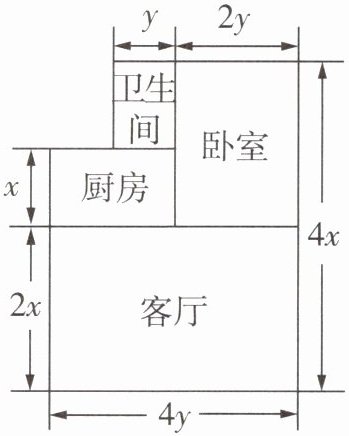
17 北师七下教材 P16 习题 T5 应用意识 (1) 一套住房的部分结构如图所示(单位：m),这套房子的主人打算把卧室以外的部分都铺上地砖,至少需要多少平方米的地砖？如果某种地砖的价格是 $a$ 元/$m^2$,那么购买所需地砖至少需要多少元？
(2) 已知 (1) 中房屋的高度为 $h$ m,现需要在客厅和卧室的墙壁上贴壁纸,那么至少需要多少平方米的壁纸？如果某种壁纸的价格是 $b$ 元/$m^2$,那么购买所需壁纸至少需要多少元(计算时不扣除门、窗所占的面积)？

答案： 解:
(1)根据题意得,需要铺地砖的区域面积为xy+x·2y+2x·4y=11xy(m²),把卧室以外的部分都铺上地砖,至少需要11xy m²的地砖.当地砖的价格是a元/m²时,购买所需地砖至少需要11axy元.
(2)根据题意得,至少需要(4x+4x+4y+4y+2y+2y)h=(8xh+12yh)m²的壁纸,当壁纸的价格是b元/m²时,至少需要(8xhb+12yhb)元.