《2025年一遍过八年级数学上册华师大版》

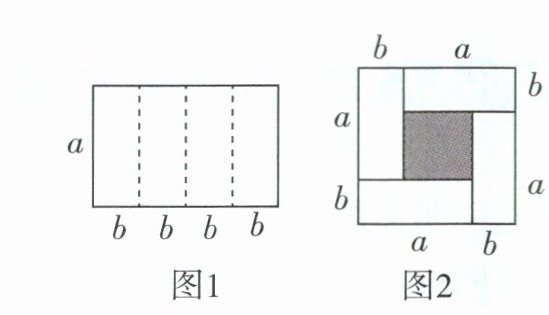
(1)观察图 1,图 2,则 $(a + b)^{2}$,$(a - b)^{2}$,$ab$ 之间的等量关系是(a+b)²-(a-b)²=4ab。
(2)根据(1)的结论，若x+y=4,xy=1,则(x-y)²的值是(12)

答案：
(1)(a+b)²-(a-b)²=4ab
(2）12

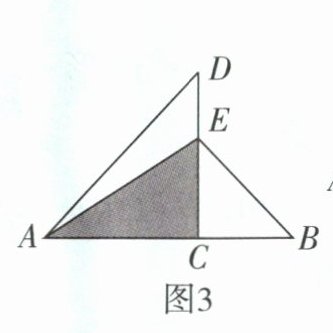
(3)如图 3,$C$ 是线段 $AB$ 上的一点,以 $AC$,$BC$ 为边,向上分别作等腰直角三角形 $ACD$ 和等腰直角三角形 $BCE$,点 $E$ 在 $CD$ 上,连接 $AE$。若 $AB = 11$,$DE = 3$,求 $\triangle ACE$ 的面积。

答案： 解：在等腰直角三角形ACD和等腰直角三角形BCE中，BC=CE，AC=CD。设AC=CD=m，BC=CE=n，则m+n=AB=11，m-n=DE=3。由
(1)，可得4mn=(m+n)²-(m-n)²=121-9=112，
∴mn=28，
∴S_△ACE=1/2 mn=14。

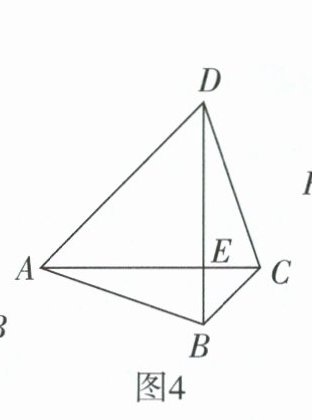
(4)如图 4,某学校有一块四边形空地 $ABCD$,$AC\perp BD$ 于点 $E$,$AE = DE$,$BE = CE$。该校计划在 $\triangle AED$ 和 $\triangle BEC$ 区域内种花,在 $\triangle CDE$ 和 $\triangle ABE$ 区域内种草。经测量,种花区域的面积之和为 $109\ m^{2}$,$AC = 16\ m$,求种草区域的面积之和。

答案： 解：设BE=CE=p，AE=DE=q，则p+q=AC=16，1/2 p²+1/2 q²=109。
∵(p+q)²=p²+q²+2pq=109×2+2pq=16²，
∴pq=19，
∴S_△ABE+S_△CDE=pq=19。
∴种草区域的面积之和为19m²。

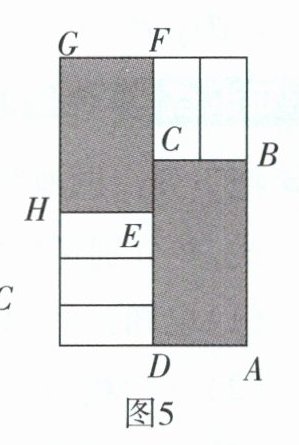
(5)利用 $5$ 张完全相同的小长方形纸片(长为 $a$、宽为 $b$)拼成如图 5 所示的大长方形,记长方形 $ABCD$ 的面积为 $S_{1}$,长方形 $EFGH$ 的面积为 $S_{2}$。若不论 $AB$ 的长为何值,$S_{1}-S_{2}$ 为定值,求 $a$ 与 $b$ 之间的数量关系。

答案： 解：根据题意，得S₁=2b(3b+CE)=6b²+2bCE，S₂=a(a+CE)=a²+aCE，
∴S₁-S₂=6b²-a²+(2b-a)CE。
∵不论AB的长为何值，S₁-S₂为定值，且AB=CE+3b，
∴S₁-S₂的值与CE无关，
∴2b-a=0，即a=2b。