第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
13 若$[(x^{3})^{m}]^{2}= x^{12}$,则$m$的值是(
A.1
B.2
C.3
D.7
B
)A.1
B.2
C.3
D.7
答案:
B
14 [2024 河北中考]若$a$,$b$是正整数,且满足$\underbrace{2^{a}+2^{a}+… +2^{a}}_{8个2^{a}相加}= \underbrace{2^{b}×2^{b}×… ×2^{b}}_{8个2^{b}相乘}$,则$a与b$的关系正确的是(
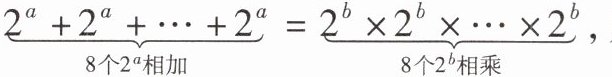
A.$a + 3 = 8b$
B.$3a = 8b$
C.$a + 3 = b^{8}$
D.$3a = 8 + b$
A
)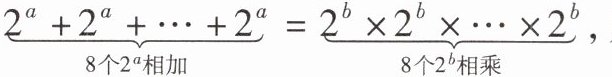
A.$a + 3 = 8b$
B.$3a = 8b$
C.$a + 3 = b^{8}$
D.$3a = 8 + b$
答案:
A
15 若$x = 2^{m}+2$,$y = 3 + 4^{m}$。
(1)请用含$x的代数式表示y$;
(2)若$x = 3$,求此时$y$的值。
(1)请用含$x的代数式表示y$;
(2)若$x = 3$,求此时$y$的值。
答案:
解:
(1)
∵x=2ᵐ+2,
∴2ᵐ=x-2.
∵4ᵐ=(2²)ᵐ=(2ᵐ)²=(x-2)²,
∴y=(x-2)²+3.
(2)当x=3时,y=(3-2)²+3=4.
(1)
∵x=2ᵐ+2,
∴2ᵐ=x-2.
∵4ᵐ=(2²)ᵐ=(2ᵐ)²=(x-2)²,
∴y=(x-2)²+3.
(2)当x=3时,y=(3-2)²+3=4.
16 [2025 保定模拟]对于两个非零的有理数$a$,$b$,定义新运算:$a\odot b = a^{b}$。若$(2\odot m)×(4\odot n)= 32$,求$m + 2n$的值。
答案:
解:
∵a⊙b=aᵇ,
∴(2⊙m)×(4⊙n)=2ᵐ×4ⁿ=32.
∵2ᵐ×4ⁿ=2ᵐ×(2²)ⁿ=2ᵐ×2²ⁿ=2ᵐ⁺²ⁿ,
∴2ᵐ⁺²ⁿ=32=2⁵,
∴m+2n=5.
∵a⊙b=aᵇ,
∴(2⊙m)×(4⊙n)=2ᵐ×4ⁿ=32.
∵2ᵐ×4ⁿ=2ᵐ×(2²)ⁿ=2ᵐ×2²ⁿ=2ᵐ⁺²ⁿ,
∴2ᵐ⁺²ⁿ=32=2⁵,
∴m+2n=5.
17 [运算能力]阅读下列材料,解决问题。
材料一:比较$3^{22}和4^{11}$的大小。
解:$\because 4^{11}= (2^{2})^{11}= 2^{22}$,$3>2$,
$\therefore 3^{22}>2^{22}$,即$3^{22}>4^{11}$。
小结:指数相同的情况下,通过比较底数(底数大于 1)的大小来确定两个幂的大小。
材料二:比较$2^{8}和8^{2}$的大小。
解:$\because 8^{2}= (2^{3})^{2}= 2^{6}$,$8>6$,
$\therefore 2^{8}>2^{6}$,即$2^{8}>8^{2}$。
小结:底数相同(底数大于 1)的情况下,通过比较指数的大小来确定两个幂的大小。
(1)比较$3^{44}$,$4^{33}$,$5^{22}$的大小;
(2)比较$81^{31}$,$27^{41}$,$9^{61}$的大小;
追问:已知$a^{2}= 2$,$b^{3}= 3$,比较$a$,$b$的大小。($a$,$b$均为大于 1 的数)
材料一:比较$3^{22}和4^{11}$的大小。
解:$\because 4^{11}= (2^{2})^{11}= 2^{22}$,$3>2$,
$\therefore 3^{22}>2^{22}$,即$3^{22}>4^{11}$。
小结:指数相同的情况下,通过比较底数(底数大于 1)的大小来确定两个幂的大小。
材料二:比较$2^{8}和8^{2}$的大小。
解:$\because 8^{2}= (2^{3})^{2}= 2^{6}$,$8>6$,
$\therefore 2^{8}>2^{6}$,即$2^{8}>8^{2}$。
小结:底数相同(底数大于 1)的情况下,通过比较指数的大小来确定两个幂的大小。
(1)比较$3^{44}$,$4^{33}$,$5^{22}$的大小;
(2)比较$81^{31}$,$27^{41}$,$9^{61}$的大小;
追问:已知$a^{2}= 2$,$b^{3}= 3$,比较$a$,$b$的大小。($a$,$b$均为大于 1 的数)
答案:
解:
(1)
∵3⁴⁴=(3⁴)¹¹=81¹¹,4³³=(4³)¹¹=64¹¹,5²²=(5²)¹¹=25¹¹,81>64>25,
∴81¹¹>64¹¹>25¹¹,即3⁴⁴>4³³>5²².
(2)
∵81³¹=(3⁴)³¹=3¹²⁴,27⁴¹=(3³)⁴¹=3¹²³,9⁶¹=(3²)⁶¹=3¹²²,124>123>122,
∴3¹²⁴>3¹²³>3¹²²,即81³¹>27⁴¹>9⁶¹.追问:
∵a²=2,b³=3,
∴a⁶=8,b⁶=9.
∵8<9,
∴a⁶<b⁶.又
∵a,b均为大于1的数,
∴a<b.
(1)
∵3⁴⁴=(3⁴)¹¹=81¹¹,4³³=(4³)¹¹=64¹¹,5²²=(5²)¹¹=25¹¹,81>64>25,
∴81¹¹>64¹¹>25¹¹,即3⁴⁴>4³³>5²².
(2)
∵81³¹=(3⁴)³¹=3¹²⁴,27⁴¹=(3³)⁴¹=3¹²³,9⁶¹=(3²)⁶¹=3¹²²,124>123>122,
∴3¹²⁴>3¹²³>3¹²²,即81³¹>27⁴¹>9⁶¹.追问:
∵a²=2,b³=3,
∴a⁶=8,b⁶=9.
∵8<9,
∴a⁶<b⁶.又
∵a,b均为大于1的数,
∴a<b.
查看更多完整答案,请扫码查看


