《2025年一遍过八年级数学上册华师大版》

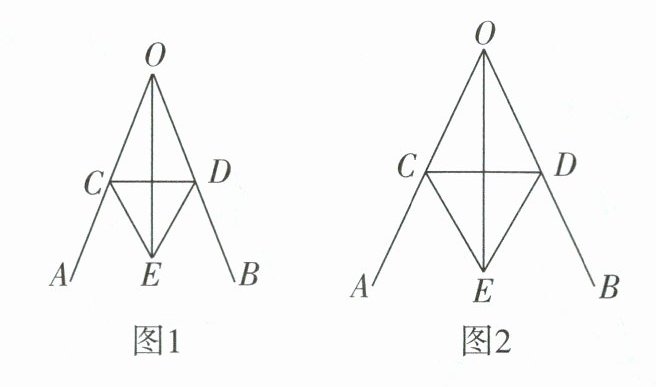
(1) 如图 1 是古希腊数学家欧几里得所著的《几何原本》第 1 卷命题 9：“平分一个已知角”即：作一个已知角的平分线。如图 2 是欧几里得在《几何原本》中给出的角平分线作图法：在 $OA$ 和 $OB$ 上分别取点 $C$,$D$,使得 $OC = OD$,连接 $CD$,以 $CD$ 为边作等边三角形 $CDE$,则 $OE$ 就是 $\angle AOB$ 的平分线。请写出 $OE$ 平分 $\angle AOB$ 的依据：SSS。

答案：
(1)SSS

(2) 小明根据以上信息研究发现：$\triangle CDE$ 不一定必须是等边三角形,只需 $CE = DE$ 即可。他查阅资料：我国古代已经用角尺平分任意角。做法如下：如图 3,在 $\angle AOB$ 的边 $OA$,$OB$ 上分别取 $OM = ON$,移动角尺,使角尺两边相同刻度分别与点 $M$,$N$ 重合,则过角尺顶点 $C$ 的射线 $OC$ 是 $\angle AOB$ 的平分线。请说明此做法的理由。

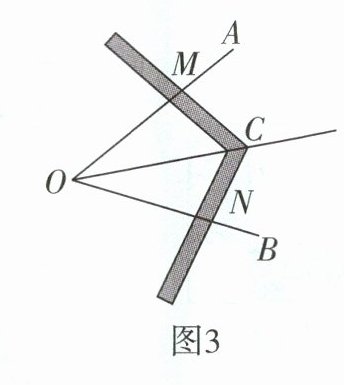
答案：
(2)在△OCM和△OCN中，
∵OM=ON,CM=CN,OC=OC,
∴△OCM≌△OCN(SSS),
∴∠AOC=∠BOC,
∴OC是∠AOB的平分线

(3) 小明将研究应用于实践,如图 4,校园的两条小路 $AB$ 和 $AC$,汇聚形成了一个岔路口 $A$,现在学校要在两条小路之间安装一盏路灯 $E$,使得路灯照亮两条小路(两条小路一样亮),并且路灯 $E$ 到岔路口 $A$ 的距离和休息椅 $D$ 到岔路口 $A$ 的距离相等。试问路灯应该安装在哪个位置？请用不带刻度的直尺和圆规在对应的示意图 5 中作出路灯 $E$ 的位置。(保留作图痕迹,不写作法)

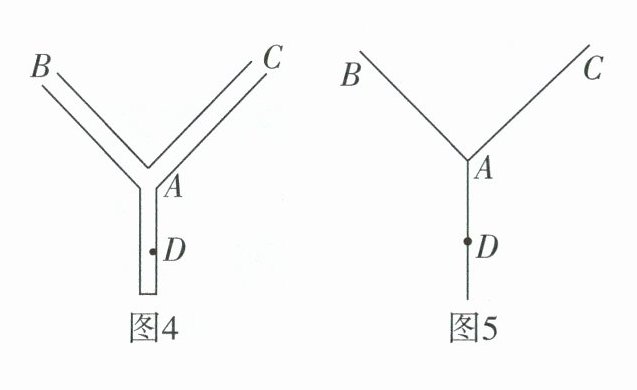
答案：

(3)如图,点E即所求.