《2025年一遍过八年级数学上册华师大版》

1 求64和-27的立方根.

答案： 解:
∵$4^{3}=64$,
∴64的立方根是4.
∵$(-3)^{3}=-27$,
∴-27的立方根是-3.

2 (1)$\sqrt{625}$的平方根是±5；

答案：
(1)±5;

(2)$\sqrt{(-9)^2}$的算术平方根是______；

答案：
(2)3;
(3)$\sqrt[3]{5}$

(3)$\sqrt[3]{125}$的立方根是______.

答案：
(3)$\sqrt[3]{5}$

3 给出下列说法：①$\frac{\sqrt{3}}{5}$是分数；②$\frac{25}{7}$是无理数；③负无限不循环小数是负无理数；④无理数包括正无理数,0,负无理数；⑤分数是有限小数；⑥无理数是无限小数；⑦有限小数是有理数.其中正确的是③⑥⑦.(填序号)

答案： ③⑥⑦

4 计算：
(1)$|\sqrt{6}-3|+|2-\sqrt{6}|$；
(2)$|\sqrt{3}-2|+|1-\sqrt{3}|-|\sqrt{6}-4|$.

答案： 解:
(1)$|\sqrt{6}-3|+|2-\sqrt{6}|=-(\sqrt{6}-3)+[-(2-\sqrt{6})]=-\sqrt{6}+3-2+\sqrt{6}=1$.
(2)$|\sqrt{3}-2|+|1-\sqrt{3}|-|\sqrt{6}-4|=-(\sqrt{3}-2)+[-(1-\sqrt{3})]-[-(\sqrt{6}-4)]=-\sqrt{3}+2-1+\sqrt{3}+\sqrt{6}-4=\sqrt{6}-3$.

5 下表是平方根和立方根的部分内容：

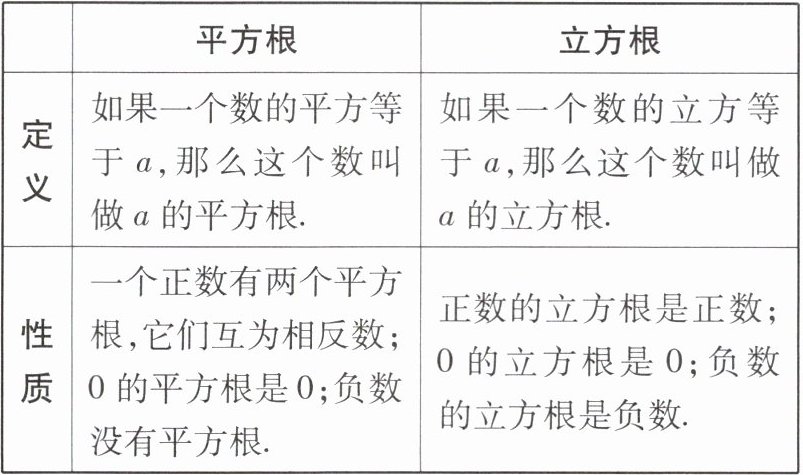
(1)类比平方根和立方根的定义,给四次方根下定义：如果一个数的四次方等于a,那么这个数叫做a的四次方根.
(2)①1的四次方根是±1,16的四次方根是±2,0的四次方根是0,-625没有(填“有”或“没有”)四次方根.
②类比平方根和立方根的性质,归纳四次方根的性质：一个正数有两个四次方根,它们互为相反数;0的四次方根是0;负数没有四次方根.
(3)$\pm\sqrt[4]{625}= $±5,$\sqrt[4]{(-\frac{1}{4})^4}= $$\frac{1}{4}$.

答案： 解:
(1)如果一个数的四次方等于a,那么这个数叫做a的四次方根
(2)①±1 ±2 0 没有②一个正数有两个四次方根,它们互为相反数;0的四次方根是0;负数没有四次方根
(3)±5 $\frac{1}{4}$

6 教材P20复习题T11变式 阅读材料并回答问题.
$\sqrt{1^3}= \sqrt{1^2}= 1$,$\sqrt{1^3+2^3}= \sqrt{3^2}= 3$,
$\sqrt{1^3+2^3+3^3}= \sqrt{6^2}= 6$,
$\sqrt{1^3+2^3+3^3+4^3}= \sqrt{10^2}= 10……$
(1)根据以上规律,写出第6个等式；
(2)若某等式的结果是55,请写出该等式；
(3)根据以上规律,写出第$n$个等式.(用含$n$的式子表示,$n$为整数,且$n\geq1$)

答案： 解:
(1)$\sqrt{1^{3}+2^{3}+3^{3}+4^{3}+5^{3}+6^{3}}=\sqrt{21^{2}}=21$.
(2)$\sqrt{1^{3}+2^{3}+3^{3}+4^{3}+5^{3}+6^{3}+7^{3}+8^{3}+9^{3}+10^{3}}=\sqrt{55^{2}}=55$.
(3)$\sqrt{1^{3}+2^{3}+3^{3}+4^{3}+5^{3}+6^{3}+\cdots+n^{3}}=\sqrt{\left[\frac{n(n+1)}{2}\right]^{2}}=\frac{n(n+1)}{2}$.