《2025年一遍过八年级数学上册华师大版》

7 [2025 温州永嘉中学附中月考]如图,在$\triangle ABC$中,$\angle B = \angle C = 60^{\circ}$,$BD = CF$,$BE = CD$,则$\angle EDF$的度数是(C)


A.$40^{\circ}$
B.$50^{\circ}$
C.$60^{\circ}$
D.$30^{\circ}$

答案： C 在△BDE和△CFD中,BD=CF,∠B=∠C,BE=CD,
∴△BDE≌△CFD(SAS),
∴∠BDE=∠CFD,
∴∠EDF=180°−(∠BDE+∠CDF)=180°−(∠CFD+∠CDF)=∠C=60°.

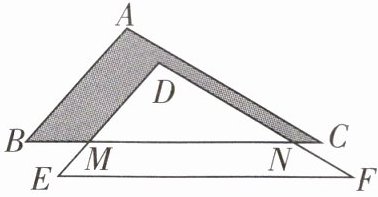
8 [2025 唐山期中]如图,已知$AC = DF$,且$AC // DF$,$BC // EF$,$BM + CN = EF - MN$。
(1)若$AB = 5$,$EM = 1$,求$DM$的值。
(2)比较图中阴影部分的面积与四边形$EMNF$的面积的大小。

答案：
(1)
∵AC//DF,
∴∠C=∠DNM.
∵BC//EF,
∴∠DNM=∠F,
∴∠C=∠F.
∵BM+CN=EF−MN,
∴EF=BM+CN+MN=BC.
在△ABC和△DEF中,
BC=EF,∠C=∠F,AC=DF,
∴△ABC≌△DEF(SAS),
∴DE=AB=5,
∵EM=1,
∴DM=DE−EM=5−1=4.
(2)
∵△ABC≌△DEF,
∴S△ABC=S△DEF.
∵S阴影部分=S△ABC−S△DMN,S四边形EMNF=S△DEF−S△DMN,
∴S阴影部分=S四边形EMNF

9 如图,工人师傅在竖直墙壁的$O$处用钻打孔,要使孔口从墙壁对面的$B$处打出,墙壁厚$35$cm,$B处与O处的高度差AB为20$cm。工人师傅在垂直于墙壁的方向上截取$OC = 35$cm,作$CD \perp OC于点C$,使$CD = 20$cm,连接$OD$,然后沿着$DO$的方向打孔,结果钻头正好从$B$处打出,这是为什么？

答案： 解:根据题意得，
OC=OA=35cm,CD=AB=20cm,∠OAB=∠OCD=90°.
在△OAB和△OCD中，
AB=CD,∠OAB=∠OCD,OA=OC,
∴△OAB≌△OCD(SAS),
∴∠AOB=∠COD.
∵OA,OC均与墙壁垂直，
∴点A,O,C在同一条直线上
∴∠AOB+∠BOC=180°,
∴∠COD+∠BOC=180°,
∴点B,O,D在同一条直线上，
∴钻头正好从B处打出.

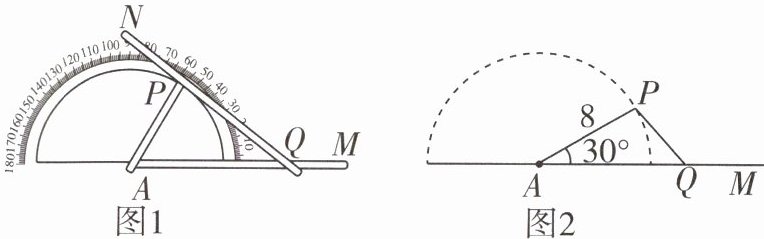
10 几何直观 [2025 北京丰台区期中]李老师制作了如图 1 所示的学具,用来探究“边边角”分别相等的两个三角形是否全等。操作学具时,点$Q在轨道槽AM$上运动,点$P既能在以点A$为圆心、以$8$为半径的半圆轨道槽上运动,也能在轨道槽$QN$上运动。图 2 是操作学具时,所对应某个位置的图形的示意图。给出下列结论：①当$\angle PAQ = 30^{\circ}$,$PQ = 6$时,可得到形状唯一确定的$\triangle PAQ$；②当$\angle PAQ = 90^{\circ}$,$PQ = 10$时,可得到形状唯一确定的$\triangle PAQ$；③当$\angle PAQ = 150^{\circ}$,$PQ = 12$时,可得到形状唯一确定的$\triangle PAQ$。其中正确的有( )


A.$0$个
B.$1$个
C.$2$个
D.$3$个

答案：
C ①当∠PAQ=30°,PQ=6时,如图1,点Q的位置有2个,且2个△PAQ的形状不一样,故①错误.②当∠PAQ=90°,PQ=10时,如图2,点Q的位置有2个,但两个△PAQ的形状一样,故②正确.③当∠PAQ=150°,PQ=12时,如图3,点Q的位置只有1个,故③正确.