《2025年一遍过八年级数学上册华师大版》

6 图 1,图 2,图 3 均是 8 × 8 的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为 1,点 A,B,C 均在格点上. 在图 1,图 2,图 3 中,只用无刻度的直尺,按下列要求画图.(不用写画法,保留作图痕迹)
(1)在图 1 中画出△ABC 的高 AD.
(2)在图 2 中的△ABC 的边 BC 上找到一点 E,连接 AE,使 AE 平分△ABC 的面积.
(3)在图 3 中画△BCF,使△ABC ≌ △FCB,其中点 F 不与点 A 重合.

答案：

(1)如图1,线段AD 即所求.
(2)如图2,线段AE 即所求.
(3)如图3,△BCF 即所求.

7 [新趋势·条件开放][2024 淄博中考] 如图,已知 AB = CD,点 E,F 在线段 BD 上,且 AF = CE. 请从①BF = DE,②∠BAF = ∠DCE,③AF = CF 中选择一个合适的选项作为已知条件,使得△ABF ≌ △CDE.
你添加的条件是 ①(或②).(只填写一个序号)
添加条件后,请证明：AE // CF.

答案： ①(或②)证明如下:当选取①时,在△ABF 与△CDE 中,AB=CD,AF=CE,BF=DE,
∴△ABF≌△CDE(SSS),
∴∠B=∠D.
∵BF=DE,
∴BF+EF=DE+EF,即BE=DF.在△ABE 与△CDF 中,AB=CD,∠B=∠D,BE=DF,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE//CF.当选取②时,在△ABF 与△CDE 中,AB=CD,∠BAF=∠DCE,AF=CE,
∴△ABF≌△CDE(SAS),
∴∠B=∠D,BF=DE,
∴BF+EF=DE+EF,即BE=DF.在△ABE 与△CDF 中,AB=CD,∠B=∠D,BE=DF,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE//CF.

8 [新趋势·尺规作图][北师七下教材 P109 习题 T16] 先画一个△ABC,然后选择△ABC 中适当的边和角,用尺规作出与△ABC 全等的三角形(在所作的三角形中标出用到的条件).

答案：
如图1,图2,△EDF≌△ABC(SAS).
　　　 　　　　
或如图3,图4,△A₁B₁C₁≌△ABC(ASA).
　　　　
或如图5,图6,△A₂B₂C₂≌△ABC(SSS).
　　　 　　　
(画出一个即可,答案不唯一)

9 [推理能力][2025 忻州期中] 下面是博学小组学习报告的部分内容,请认真阅读,并完成下面的问题.
【一般定义】
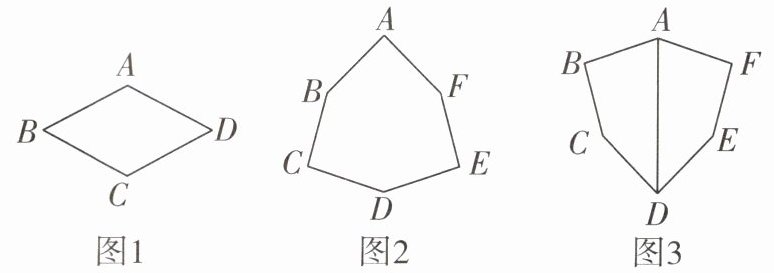
对于一个边数为偶数的凸多边形,若其各边都相等,相间的角相等、相邻的角不相等,就称该凸多边形为等边半正多边形. 如图 1 就是等边半正四边形,类似地,还有等边半正六边形、等边半正八边形……
【特例研究】
如图 2,若六边形 ABCDEF 是等边半正六边形,则 AB = BC = CD = DE = EF = FA,∠A = ∠C = ∠E,∠B = ∠D = ∠F,且∠A ≠ ∠B.
(1)等边半正六边形相邻的两个内角的和为 °.
(2)在图 2 中作一个等边半正四边形.(保留作图痕迹,不写画法)
(3)如图 3,六边形 ABCDEF 是等边半正六边形,连接对角线 AD,猜想∠BAD 与∠FAD 的数量关系,并说明理由.

答案：

(1)240
∵六边形的内角和为(6-2)×180°=720°,且∠A=∠C=∠E,∠B=∠D=∠F,
∴等边半正六边形相邻两个内角的和为720°÷3=240°.
(2)如图1,四边形CDEG 即所求.
　　　　 　　
(3)∠BAD=∠FAD.理由如下:如图2,连接BD,FD.
∵六边形ABCDEF 是等边半正六边形,
∴AB=BC=CD=DE=EF=FA,∠C=∠E.在△BCD 和△FED 中,BC=FE,∠C=∠E,CD=ED,
∴△BCD≌△FED(SAS),
∴BD=FD.在△ABD 和△AFD 中,AB=AF,BD=FD,AD=AD,
∴△BAD≌△FAD(SSS),
∴∠BAD=∠FAD.