《2025年一遍过八年级数学上册华师大版》

9 [2024广州中考]下列图案中,点$O$为正方形的中心,阴影部分的两个三角形全等,则阴影部分的两个三角形关于点$O$对称的是(C)

答案： C

10 全等三角形也称合同三角形,平面内的合同三角形分为真正合同三角形(如图1)和镜面合同三角形(如图2).下列各组合同三角形中,是镜面合同三角形的是①③.(填序号)

答案： ①③

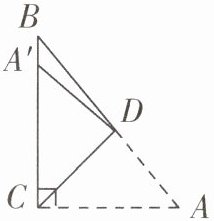
11 如图,在直角三角形$ABC$中,$\angle ACB= 90^{\circ}$,$\angle A= 50^{\circ}$,将$\triangle ABC$折叠,使点$A落在CB边上A'$处,折痕为$CD$,则$\angle A'DB= $10$^{\circ}$.

答案： 10 由题意知△ADC≌△A'DC,
∴∠CA'D=∠A=50°.
∵∠A=50°,∠ACB=90°,
∴∠B=90°-∠A=40°.
∵∠CA'D=∠B+∠A'DB,
∴∠A'DB=∠CA'D-∠B=50°-40°=10°.

12 易错题 一个三角形的三边长分别是4,9,10,另一个三角形三边的长分别是4,$2x - 3y$,$3x - y$.若这两个三角形全等,则$x + y$的值为2或$\frac{5}{7}$.

答案： 2或$\frac{5}{7}$ 根据题意,得$\left\{\begin{array}{l} 2x-3y=9,\\ 3x-y=10\end{array}\right. $或$\left\{\begin{array}{l} 2x-3y=10,\\ 3x-y=9,\end{array}\right. $解得$\left\{\begin{array}{l} x=3,\\ y=-1\end{array}\right. $或$\left\{\begin{array}{l} x=\frac {17}{7},\\ y=-\frac {12}{7}\end{array}\right. $,
∴x+y的值为2或$\frac{5}{7}$.

13 如图,$\triangle ABD\cong\triangle EBC$,点$A$,$B$,$C$在同一条直线上,点$E在BD$上,$AB= 2\ cm$,$BC= 3\ cm$.
(1)求$DE$的长；
(2)判断$AC与BD$的位置关系,并说明理由；
(3)判断$AD与直线CE$的位置关系,并说明理由.

答案：
解:
(1)
∵△ABD≌△EBC,
∴BD=BC=3cm,BE=AB=2cm,
∴DE=BD-BE=1cm.
(2)AC⊥BD.理由如下:
∵△ABD≌△EBC,
∴∠ABD=∠EBC.
∵点A,B,C在同一条直线上,
∴∠ABD+∠EBC=180°,
∴∠EBC=90°,
∴AC⊥BD.
(3)AD⊥直线CE.理由如下:
如图,延长CE交AD于点F.
∵△ABD≌△EBC,
∴∠D=∠C.
在Rt△ABD中,∠A+∠D=90°,
∴∠A+∠C=90°,
∴∠AFC=90°,
∴CE⊥AD.

14 推理能力 [2025海东期末]如图,在$\triangle ABC$中,$\angle B= \angle C$,$BC= 10\ cm$,点$D在AB$上,$BD= 6\ cm$,点$M从点B出发以1\ cm/s的速度向点C$运动,同时,点$N从C出发向点A$运动,设运动时间为$t\ s$,连接$DM$,$MN$.
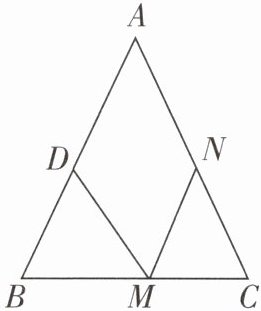
(1)$BM= $t$cm$,$MC= $______10-t$cm$.(用含$t$的式子表示)
(2)若点$N的运动速度为1\ cm/s$,当$\triangle DBM\cong\triangle MCN$时,$t$的值是多少？
(3)若点$N和点M$的运动速度不相等,要使$\triangle DBM和\triangle NCM$全等,则点$N$的运动速度应为多少？此时$t$的值是多少？

答案： 解:
(1)t (10-t)
(2)根据题意,得BM=NC=t cm.
∵△DBM≌△MCN,
∴MC=BD=6 cm,
∴10-t=6,解得t=4.
(3)已知△DBM和△NCM全等,∠B=∠C,
∴点B和点C对应,BM和MC或CN对应.
根据题意,得BM≠NC,
∴BM=MC,NC=BD=6 cm,
∴t=10-t,
∴t=5,
∴点N的运动速度为$\frac{6}{5}$cm/s.