《2025年一遍过八年级数学上册华师大版》

1 [2025无锡期末]若等腰三角形的顶角是40°,则它的一个底角的度数是(C)

A.40°
B.50°
C.70°
D.100°

答案： C
∵等腰三角形的顶角是40°,
∴它的一个底角的度数是$\frac{1}{2}×(180^{\circ}-40^{\circ})=70^{\circ}.$

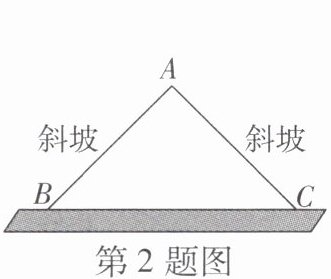
2 [2025北京期中]如图,为了让两个斜坡AB,AC与地面所成的两个锐角相同,工程人员在修斜坡时,只需让斜坡AB等于斜坡AC即可,这种操作的依据是等边对等角.

答案： 等边对等角

3 [2024绥化中考]如图,AB//CD,∠C= 33°,OC= OE,则∠A= ______°.

66

答案： 66
∵OC=OE,∠C=33°,
∴∠E=∠C=33°,
∴∠DOE=∠E+∠C=66°(三角形的一个外角等于与它不相邻的两个内角的和).
∵AB//CD,
∴∠A=∠DOE=66°.

4 [教材P99习题T2变式][2025北京工业大学实验学校期中]等腰三角形的顶角度数比一个底角度数的2倍多20°,则这个底角的度数是40°.

答案： 40° 设该等腰三角形一个底角的度数为x,则该等腰三角形的顶角度数为2x+20°,
∴2x+2x+20°=180°(三角形的内角和为180°),
∴x=40°.

5 [易错题]在证明“等边对等角”这一性质定理时,亮亮给出了如下证明思路：如图,在△ABC中,AB= AC,作∠BAC的平分线AD,利用“SAS”可证明△ABD≌△ACD,从而得出∠B= ∠C.数学兴趣小组的同学们积极思考,又发现了不同的证明思路：①过点A作AD⊥BC于点D,利用“HL”证明△ABD≌△ACD,从而得出∠B= ∠C；②作BC边的中线AD,利用“SSS”证明△ABD≌△ACD,从而得出∠B= ∠C；③过点A作AD⊥BC且平分BC,利用“ASA”证明△ABD≌△ACD,从而得出∠B= ∠C.
(1)以上证明思路正确的是②.(填序号)
(2)请你选择一个你认为正确的证明思路,写出证明过程.
]

选思路②.证明:在△ABD和△ACD中,AB=AC,AD=AD,BD=CD,
∴△ADB≌△ADC(SSS),
∴∠B=∠C(全等三角形的对应角相等).

答案： 解:
(1)②
∵要用“等边对等角”这一性质定理证明“HL”定理,
∴用“HL”定理证明“等边对等角”这一性质定理属于循环证明,故①错误;过点A作AD⊥BC时,AD不一定平分BC,故③错误.
(2)选思路②.证明:在△ABD和△ACD中,AB=AC,AD=AD,BD=CD,
∴△ADB≌△ADC(SSS),
∴∠B=∠C(全等三角形的对应角相等).

6 [2025洛阳期中]如图,已知等腰三角形ABC,AB= AC,D是边BC上的一点,下列条件不能说明AD是△ABC的角平分线的是(C)

A.∠ADB= ∠ADC
B.BD= CD
C.BC= 2AD
D.∠BAD= ∠DAC

答案： C A选项,
∵∠ADB=∠ADC,∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,
∴AD是△ABC的高.
∵△ABC是等腰三角形,
∴AD是△ABC的角平分线.B选项,
∵BD=CD,
∴AD是△ABC的中线.
∵△ABC是等腰三角形,
∴AD是△ABC的角平分线.D选项,
∵∠BAD=∠DAC,
∴AD是△ABC的角平分线.

7 [2025宿迁期中]如图,在三角测平架中,AB= AC,在BC的中点D处挂上一个重锤,让它自然垂下.若调整架身,使重锤线经过点A,则确认BC处于水平位置.这种做法的依据是等腰三角形的三线合一.

答案： 等腰三角形的三线合一

8 如图,在△ABC中,AB= AC,AD是∠BAC的平分线,AD= 8cm,BC= 6cm,点E,F是AD上的两点,则图中阴影部分的面积是12 cm².

答案： 12 cm²
∵AB=AC,AD是∠BAC的平分线,
∴BD=DC,AD⊥BC,
∴点B,C关于直线AD对称,
∴△CEF和△BEF关于直线AD对称,
∴S△BEF=S△CEF.
∵△ABC的面积是$\frac{1}{2}BC\cdot AD=\frac{1}{2}×6×8=24(cm^{2})$,
∴题图中阴影部分的面积是$\frac{1}{2}S_{\triangle ABC}=12\ cm^{2}.$

9 [2024宜宾中考]如图,点D,E分别是等边三角形ABC的边BC,AC上的点,且BD= CE,BE与AD交于点F.求证：AD= BE.
]

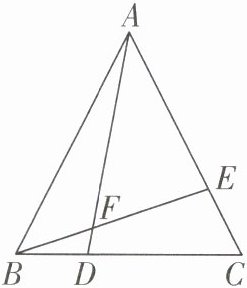
答案： 证明:
∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE=60°(等边三角形的三边相等,且每个角都等于60°).在△ABD和△BCE中,AB=BC,∠ABD=∠BCE,BD=CE,
∴△ABD≌△BCE(SAS),
∴AD=BE(全等三角形的对应边相等).