《2025年同步测控优化设计九年级数学全一册人教版福建专版》

2. 用反证法证明“在一个三角形中,至少有一个内角大于或等于$60^{\circ}$”时,可先假设“______”,然后经证明与“______”相矛盾,所以原命题成立。

答案： 三角形的三个内角都小于60°　三角形内角和定理

3. 如图,$\triangle ABC是\odot O$的内接正三角形,点$O$是圆心,点$D$,$E分别在边AC$,$AB$上,若$DA = EB$,则$\angle DOE$的度数是______度。

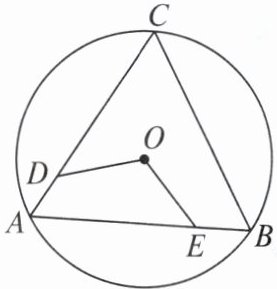
答案： 120

1. 用反证法证明“两条直线相交只有一个交点”应该先假设( )

A.两条直线相交至少有两个交点
B.两条直线相交没有两个交点
C.两条直线平行时也有一个交点
D.两条直线平行没有交点

答案： A

2. 如图,在平面直角坐标系中,点$A$,$B$,$C的坐标分别为(1,4)$,$(5,4)$,$(1,-2)$,则$\triangle ABC$外接圆的圆心坐标是( )


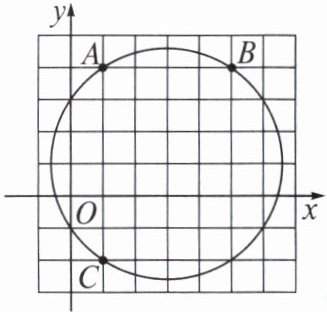
A.$(2,3)$
B.$(3,2)$
C.$(1,3)$
D.$(3,1)$

答案： D

3. 有两个圆的圆心都是点$O$,其半径分别是$2cm和6cm$,若点$P$在小圆外且在大圆内,则$OP$的取值范围是______。

答案： 2cm＜OP＜6cm　因为点P在小圆外,所以OP＞2cm.又点P在大圆内，所以OP＜6cm.

4. 由两个长方形组成的工件平面图(单位：$mm$)如图所示,直线$l$是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是______$mm$。

答案：
50　如图，设过A,B,C三点的外接圆的圆心为O,由对称性可知直线l经过圆心O,且点C的对称点D也一定在圆上，即圆O为完全覆盖这个平面图形的最小圆(包含其内部).连接AO,CO.由垂径定理(或对称性),得CM=30，AN=40.
∵CM²＋OM²＝AN²＋ON²，
∴30²＋OM²＝40²＋(70－OM)²，解得OM=40.
∴OC=√(30²＋40²)=50.即能完全覆盖这个平面图形的圆面的最小半径是50mm.

★5. 已知线段$AB和直线l$,过$A$,$B$两点作圆,并且使圆心在直线$l$上。
(1)当$AB // l$时,这样的圆能作几个？
(2)当$AB与直线l$斜交时,这样的圆能作几个？
(3)当$AB与直线l$垂直,且直线$l不过线段AB$的中点时,这样的圆能作几个？
(4)当直线$l是线段AB$的垂直平分线时,这样的圆能作几个？

答案：
解
(1)当AB//l时，线段AB的垂直平分线与直线l有唯一的公共点，这样的圆可作一个.如图①.
(2)当AB与直线l斜交时，线段AB的垂直平分线与直线l有唯一的公共点，这样的圆可作一个.如图②.
(3)当AB与直线l垂直，且直线l不过线段AB的中点时，线段AB的垂直平分线与直线l没有公共点，这样的圆不存在.如图③.
(4)当直线l是线段AB的垂直平分线时，直线l上的任一点都可作圆心，这样的圆有无数个.如图④.

1. 直线和圆有两个公共点,这时我们说这条直线和圆______,这条直线叫做圆的______；直线和圆只有一个公共点,这时我们说这条直线和圆______,这条直线叫做圆的______,这个点叫做______；直线和圆没有公共点,这时我们说这条直线和圆______。

答案： 相交　割线　相切　切线　切点　相离