《2025年同步测控优化设计九年级数学全一册人教版福建专版》

★6. 由于受干旱的影响,5月份,某市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如下表：
|周数 $ x $|1|2|3|4|
|价格 $ y $/(元/千克)|2|2.2|2.4|2.6|

进入6月,由于本地蔬菜的上市,此种蔬菜的平均销售价格 $ y $(单位：元/千克)从6月第1周的2.8元/千克下降至第2周的2.4元/千克,且 $ y $ 与周数 $ x $ 的变化情况满足二次函数 $ y = - \frac{1}{20}x^{2} + bx + c $。
(1) 请观察题中的表格,用所学过的一次函数或二次函数的有关知识直接写出5月份 $ y $ 与 $ x $ 的函数解析式,并求出6月份 $ y $ 与 $ x $ 的函数解析式；
(2) 若5月份此种蔬菜的进价 $ m $(单位：元/千克)与周数 $ x $ 之间的关系式为 $ m = \frac{1}{4}x + 1.2 $,6月份此种蔬菜的进价 $ m $(单位：元/千克)与周数 $ x $ 之间的关系式为 $ m = - \frac{1}{5}x + 2 $。试问5月份与6月份分别在哪一周销售此种蔬菜1千克的利润最大？最大利润分别是多少？

答案：
(1)通过观察可见5月份价格$y$与周数$x$符合一次函数解析式,即$y=0.2x+1.8$.
将$(1,2.8)$,$(2,2.4)$代入$y=-\dfrac{1}{20}x^{2}+bx+c$,
可得$\begin{cases} 2.8=-\dfrac{1}{20}+b+c, \\2.4=-\dfrac{1}{5}+2b+c, \end{cases}$解之,得$\begin{cases} b=-\dfrac{1}{4}, \\c=3.1, \end{cases}$
即$y=-\dfrac{1}{20}x^{2}-\dfrac{1}{4}x+3.1$.
(2)设5月份第$x$周销售此种蔬菜1千克的利润为$W_{1}$元,6月份第$x$周销售此种蔬菜1千克的利润为$W_{2}$元,$W_{1}=(0.2x+1.8)-\left(\dfrac{1}{4}x+1.2\right)=-0.05x+0.6$,因为$-0.05＜0$,所以$W_{1}$随$x$的增大而减小.
所以当$x=1$时,$W_{1最大}=-0.05+0.6=0.55$.
$W_{2}=\left(-0.05x^{2}-0.25x+3.1\right)-\left(-\dfrac{1}{5}x+2\right)=-0.05x^{2}-0.05x+1.1$.
因为其图象的对称轴为直线$x=-\dfrac{-0.05}{2×(-0.05)}=-0.5$,且$-0.05＜0$,所以当$x＞-0.5$时,$y$随$x$的增大而减小.
所以当$x=1$时,$W_{2最大}=1$.
所以5月份销售此种蔬菜1千克的利润在第1周最大,最大利润为0.55元;6月份销售此种蔬菜1千克的利润在第1周最大,最大利润为1元.

1. 二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数。通常以抛物线的顶点为____,以抛物线的对称轴为____建立平面直角坐标系。

答案： 原点　y轴

2. 某广场有一喷水池,水从地面喷出,如图,以水平地面为$x$轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线$y = -x^{2}+4x$的一部分,则水喷出的最大高度是( )


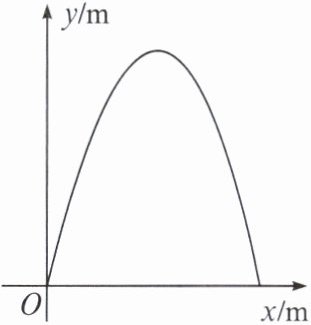
A.$4m$
B.$3m$
C.$2m$
D.$1m$

答案： A

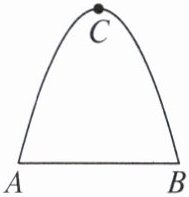
3. 有一大门是抛物线形水泥建筑物,如图,大门地面宽$AB为4m$,顶部$C离地面高度为4.4m$。现在一辆装满货物的汽车欲通过大门,货物顶部距地面$2.8m$,装货宽度为$2.4m$。请你通过计算,判断这辆汽车能否顺利通过大门。

答案： 解不妨以AB的中点O为原点，AB所在直线为x轴，建立平面直角坐标系，则A(-2,0),B(2,0),C(0,4.4).设抛物线的解析式为y=ax²+4.4,把B(2,0)代入，得4a+4.4=0,a=-1.1.所以y=-1.1x²+4.4.由抛物线的对称性，当x=2.4÷2=1.2时，y=2.816＞2.8.所以这辆汽车能顺利通过大门.