《2025年同步测控优化设计九年级数学全一册人教版福建专版》

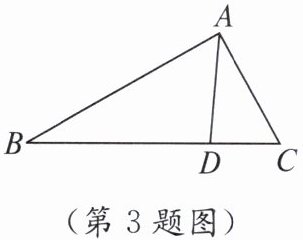
3. 如图,已知点 $D$ 是$\triangle ABC$的边 $BC$ 上任一点,$AB = 4$,$AD = 2$,$\angle DAC= \angle B$。若$\triangle ABD$的面积为 $a$,则$\triangle ACD$的面积为( )

A.$a$
B.$\frac{1}{2}a$
C.$\frac{1}{3}a$
D.$\frac{2}{5}a$

答案： C $\because \angle DAC=\angle B$,$\angle C=\angle C$,$\therefore \triangle ACD\backsim \triangle BCA$. $\therefore \frac{AD}{AB}=\frac{2}{4}=\frac{1}{2}$. 因此$\triangle ACD$与$\triangle BCA$的相似比是$\frac{1}{2}$,即面积比是$\frac{1}{4}$.设$\triangle ACD$的面积为S,则$\triangle ABC$的面积为$S+a$,因此$\frac{S}{S+a}=\frac{1}{4}$,解得$S=\frac{1}{3}a$.

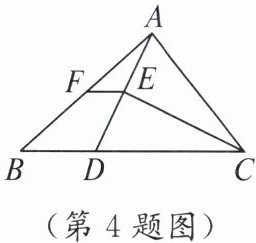
4. 如图,在$\triangle ABC$中,已知 $BC＞AC$,点 $D$ 在 $BC$ 上,且 $DC = AC$,$\angle ACB$的平分线 $CE$ 交 $AD$ 于点 $E$,点 $F$ 是 $AB$ 的中点,则 $S_{\triangle AEF}:S_{四边形BDEF}$为( )

A.$3:4$
B.$1:2$
C.$2:3$
D.$1:3$

答案： D $\because DC=AC$,CE平分$\angle ACB$, $\therefore AE=DE$(等腰三角形"三线合一"). $\because$点F是AB的中点, $\therefore EF$是$\triangle ABD$的中位线, $\therefore EF// BD$,$EF=\frac{1}{2}BD$. $\therefore \triangle AFE\backsim \triangle ABD$. 则$S_{\triangle AEF}:S_{\triangle ADB}=(\frac{EF}{DB})^{2}=(\frac{1}{2})^{2}=\frac{1}{4}$, $\therefore S_{\triangle AEF}:S_{四边形BDEF}=1:3$,应选D.

5. 在$\triangle ABC$中,已知 $D$,$E$ 分别是边 $AB$ 与 $AC$ 的中点,$BC = 4$,下面四个结论：① $DE = 2$；②$\triangle ADE\backsim\triangle ABC$；③$\triangle ADE的面积与\triangle ABC$的面积之比为 $1:4$；④$\triangle ADE的周长与\triangle ABC$的周长之比为 $1:4$；⑤$\triangle ADE与\triangle ABC$对应线段的比为 $1:2$,其中正确的有____。(填序号)

答案： ①②③⑤ $\because$D,E分别是边AB与AC的中点,$\therefore DE// BC$,且$DE=\frac{1}{2}BC$.又$BC=4$,$\therefore DE=2$,即①正确;由$DE// BC$,$\therefore \triangle ADE\backsim \triangle ABC$,即②正确;由$\triangle ADE\backsim \triangle ABC$和$DE=\frac{1}{2}BC$,得$\triangle ADE$的面积与$\triangle ABC$的面积之比为1:4,且易求$\triangle ADE$的周长与$\triangle ABC$的周长之比为1:2,$\therefore$③正确,④错误;显然,⑤也正确,故正确的有①②③⑤.

6. 如图,在$\triangle ABC$中,$M$,$N$ 分别为 $AC$,$BC$ 的中点。若 $S_{\triangle CMN}= 1$,则 $S_{四边形ABNM}= $____。

答案： 3 $\because$M,N分别为AC,BC的中点, $\therefore MN// AB$,且$MN=\frac{1}{2}AB$, $\therefore \triangle CMN\backsim \triangle CAB$,且相似比为1:2, $\therefore \frac{S_{\triangle CMN}}{S_{\triangle CAB}}=\frac{1}{4}$. $\because S_{\triangle CMN}=1$,$\therefore S_{\triangle CAB}=4$, $\therefore S_{四边形ABNM}=S_{\triangle CAB}-S_{\triangle CMN}=4-1=3$.

1. 已知两个相似三角形对应边上的中线的比为 $3:2$,则其相应面积之比为( )

A.$\sqrt{3}:\sqrt{2}$
B.$3:2$
C.$9:4$
D.不能确定

答案： C

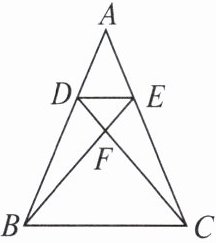
2. 如图,已知 $D$,$E$ 分别是$\triangle ABC$ 的边 $AB$,$AC$ 上的点,且 $DE// BC$,$BE$ 交 $DC$ 于点 $F$。若 $EF:FB = 1:3$,则$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}$的值为( )


A.$\frac{1}{3}$
B.$\frac{1}{9}$
C.$\frac{\sqrt{3}}{3}$
D.$\frac{1}{27}$

答案： B 由$\triangle DEF\backsim \triangle CBF$,求得$\frac{ED}{BC}=\frac{EF}{FB}=\frac{1}{3}$,再由$\triangle ADE\backsim \triangle ABC$,求得$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=(\frac{1}{3})^{2}=\frac{1}{9}$.

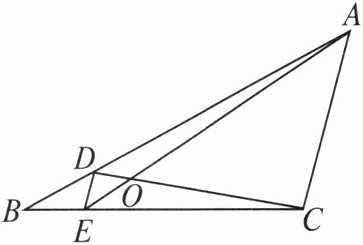
3. 如图,已知 $D$,$E$ 分别是$\triangle ABC$ 的边 $AB$,$BC$ 上的点,且 $DE// AC$,$AE$,$CD$ 相交于点 $O$,若 $S_{\triangle DOE}:S_{\triangle COA}= 1:25$,则 $S_{\triangle BDE}$与 $S_{\triangle CDE}$的比是( )


A.$1:3$
B.$1:4$
C.$1:5$
D.$1:25$

答案： B 由$DE// AC$,可得$\triangle DOE\backsim \triangle COA$,$\triangle BDE\backsim \triangle BAC$,而$\triangle DOE$与$\triangle COA$的面积比为1:25,所以这两个三角形的相似比为1:5,即$DE:CA=1:5$.根据$\triangle BDE\backsim \triangle BAC$,得$BE:BC=DE:CA=1:5$,所以$BE:EC=1:4$.因为$\triangle BDE$与$\triangle CDE$的高相等,底边$BE:EC=1:4$,所以$S_{\triangle BDE}$与$S_{\triangle CDE}$的比是1:4.

4. 如图,在$□ ABCD$中,$P$ 为边 $AD$ 上的一点,$E$,$F$ 分别是 $PB$,$PC$ 的中点,$\triangle PEF$,$\triangle PDC$,$\triangle PAB$ 的面积分别为 $S$,$S_1$,$S_2$。若 $S = 2$,则 $S_1 + S_2= $____。

答案： 8 由于E,F分别是PB,PC的中点,根据中位线的性质知$EF// BC$,且$EF=\frac{1}{2}BC$.易得$\triangle PEF\backsim \triangle PBC$,且其面积的比是1:4.由$S=2$,得$\triangle PBC$的面积为8.又根据平行四边形的性质,把$S_{1}+S_{2}$看作整体,求得$S_{1}+S_{2}=S_{\triangle PBC}=8$.

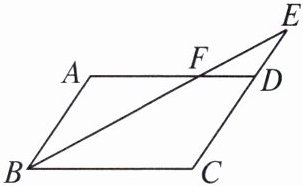
5. 如图,在$□ ABCD$中,$E$ 是 $CD$ 的延长线上一点,$BE$ 与 $AD$ 交于点 $F$,$DE= \frac{1}{2}CD$。
(1) 求证：$\triangle ABF\backsim\triangle CEB$；
(2) 若$\triangle DEF$的面积为 $2$,求$□ ABCD$的面积。

答案：
(1)证明 $\because$四边形ABCD是平行四边形, $\therefore \angle A=\angle C$,$AB// CD$. $\therefore \angle ABF=\angle CEB$, $\therefore \triangle ABF\backsim \triangle CEB$.
(2)解 $\because$四边形ABCD是平行四边形, $\therefore AD// BC$,$AB\equalparallel CD$. $\therefore \triangle DEF\backsim \triangle CEB$,$\triangle DEF\backsim \triangle ABF$. $\because DE=\frac{1}{2}CD$, $\therefore \frac{S_{\triangle DEF}}{S_{\triangle CEB}}=(\frac{DE}{EC})^{2}=\frac{1}{9}$,$\frac{S_{\triangle DEF}}{S_{\triangle ABF}}=(\frac{DE}{AB})^{2}=\frac{1}{4}$. $\because S_{\triangle DEF}=2$, $\therefore S_{\triangle CEB}=18$,$S_{\triangle ABF}=8$. $\therefore S_{四边形BCDF}=S_{\triangle BCE}-S_{\triangle DEF}=16$. $\therefore S_{四边形ABCD}=S_{四边形BCDF}+S_{\triangle ABF}=16+8=24$.

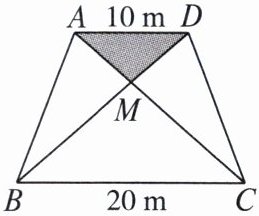
6. 某社区拟筹资金 $2000$ 元,计划在一块上、下底分别是 $10\mathrm{m}$,$20\mathrm{m}$ 的梯形空地上种植花木(如图所示),他们想在$\triangle AMD和\triangle BMC$地带种植价格为 $10$ 元/平方米的太阳花。当$\triangle AMD$地带种满花后,已经花了 $500$ 元,请你预算一下,若继续在$\triangle BMC$地带种植同样的太阳花,资金是否够用？并说明理由。

答案： 解 不够用.理由:在梯形ABCD中,$AD// BC$, 所以$\triangle AMD\backsim \triangle CMB$. 因为$AD=10\ m$,$BC=20\ m$, 所以$\frac{S_{\triangle AMD}}{S_{\triangle BMC}}=(\frac{10}{20})^{2}=\frac{1}{4}$. 因为$S_{\triangle AMD}=500÷ 10=50(m^{2})$, 所以$S_{\triangle BMC}=200\ m^{2}$. 还需要资金$200× 10=2000$(元),而剩余资金为$2000-500=1500＜2000$,所以资金不够用.