《2025年同步测控优化设计九年级数学全一册人教版福建专版》

1. 生产季节性产品的企业,当它的产品无利润时就会及时停产。现有一生产季节性产品的企业,其一年中每月获得的利润 $ y $ 和月份 $ n $ 之间的函数解析式为 $ y = - n^{2} + 14n - 24 $,则该企业一年中应停产的月份是( )

A.1月、2月、3月
B.2月、3月、4月
C.1月、2月、12月
D.1月、11月、12月

答案： C

2. 如图,在正方形 $ ABCD $ 中,$ AB = 8cm $,对角线 $ AC $,$ BD $ 相交于点 $ O $,点 $ E $,$ F $ 分别从 $ B $,$ C $ 两点同时出发,以 $ 1cm/s $ 的速度沿 $ BC $,$ CD $ 运动,到点 $ C $,$ D $ 时停止运动。设运动时间为 $ t $(单位：s),$ \triangle OEF $ 的面积为 $ S $(单位：$ cm^{2} $),则 $ S $ 与 $ t $ 的函数关系可用图象表示为( )

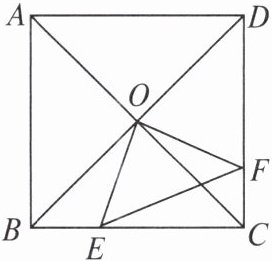
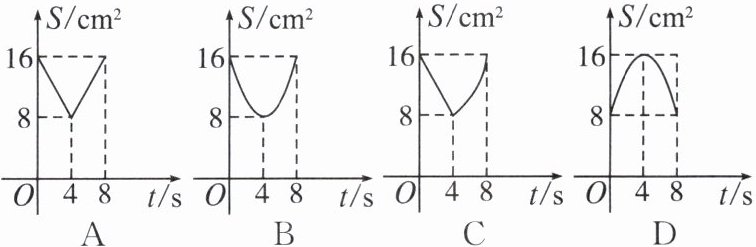
答案： B

3. 某果园有100棵橘子树,平均每一棵树结600个橘子。根据经验估计,每多种一棵树,平均每棵树就会少结5个橘子。设果园增种 $ x $ 棵橘子树,果园橘子总个数为 $ y $,则果园里增种 ____ 棵橘子树,橘子总个数最多。

答案： 10

4. 某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用 $ a $ 元($ a ＞ 0 $)。未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元。通过市场调研发现,该时装单价每降1元,每天销量增加4件。在这30天内,要使每天缴纳电商平台推广费用后的利润随天数 $ t $($ t $ 为正整数)的增大而增大,$ a $ 的取值范围应为 ____ 。

答案： $0＜a＜6$

5. 某自行车店在销售某型号自行车时,以高出进价的50%标价。已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同。
(1) 求该型号自行车的进价和标价分别是多少元？
(2) 若该型号自行车的进价不变,按(1)中的标价出售,则该店平均每月可售出51辆；若每辆自行车每降价20元,则每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大？最大利润是多少？

答案：
(1)设进价为$x$元,则标价是$1.5x$元,
由题意,得$1.5x×0.9×8-8x=(1.5x-100)×7-7x$,
解得$x=1000$,$1.5×1000=1500$.
$\therefore$进价为1000元,标价为1500元.
(2)设该型号自行车降价$a$元,利润为$w$元,由题意,得$w=\left(51+\dfrac{a}{20}×3\right)(1500-1000-a)=-\dfrac{3}{20}(a-80)^{2}+26460$.
$\because -\dfrac{3}{20}＜0$,$\therefore$当$a=80$时,$w_{最大}=26460$.
$\therefore$该型号自行车降价80元出售每月获利最大,最大利润是26460元.