《2025年同步测控优化设计九年级数学全一册人教版福建专版》

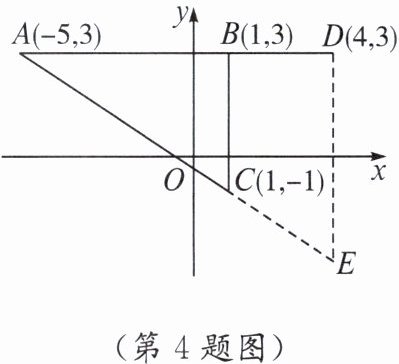
4. 已知点 $ A $,$ B $,$ C $,$ D $ 的坐标如图所示,$ E $ 是图中两条虚线的交点($ DE \perp x $ 轴)。若 $ \triangle ABC $ 和 $ \triangle ADE $ 相似,则点 $ E $ 的坐标是____。

答案： (4, -3)　由△ABC∽△ADE，且DE⊥x轴，
∴BC//DE，
∴$\frac{AB}{AD}=\frac{BC}{DE}$，得DE = 6.
∴点E的坐标为(4, -3).

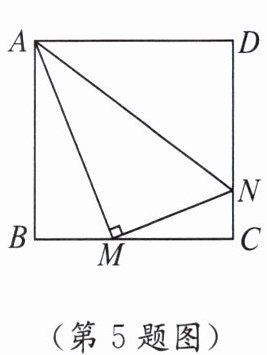
5. 已知正方形 $ ABCD $ 的边长为 $ 4 $,$ M $,$ N $ 分别是 $ BC $,$ CD $ 上的两个动点,且始终保持 $ AM \perp MN $。当 $ BM = $____时,四边形 $ ABCN $ 的面积最大。

答案： 2　设BM = x，则MC = 4 - x，当AM⊥MN时，利用互余关系可证△ABM∽△MCN，所以$\frac{AB}{MC}=\frac{BM}{CN}$，即$\frac{4}{4 - x}=\frac{x}{CN}$，得$CN=x-\frac{x^2}{4}$. 而$S_{四边形ABCN}=\frac{1}{2}(x-\frac{x^2}{4}+4)×4=-\frac{x^2}{2}+2x+8=-\frac{1}{2}(x - 2)^2+10$，故当x = 2时，四边形ABCN的面积最大.

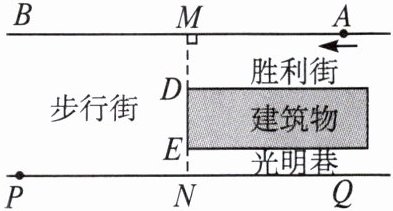
6. 如图,一段街道的两边缘所在直线分别为 $ AB $,$ PQ $,并且 $ AB // PQ $。建筑物的一端 $ DE $ 所在的直线 $ MN \perp AB $ 于点 $ M $,交 $ PQ $ 于点 $ N $。小亮从胜利街的 $ A $ 处,沿着 $ AB $ 方向前进,小明一直站在点 $ P $ 的位置等候小亮。
(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点 $ C $ 标出)；
(2)若 $ MN = 20 $ m,$ MD = 8 $ m,$ PN = 24 $ m,求(1)中的点 $ C $ 到胜利街口的距离 $ CM $。

答案：

(1)如图，CP为视线，点C为所求位置.

(2)因为AB//PQ，MN⊥AB于点M，交PQ于点N，所以∠CMD = ∠PND = 90°.
又因为∠CDM = ∠PDN，所以△CDM∽△PDN，所以$\frac{CM}{PN}=\frac{MD}{ND}$.
而MN = 20m，MD = 8m，PN = 24m，即$\frac{CM}{24}=\frac{8}{12}$，所以CM = 16m，
即点C到胜利街口的距离CM为16m.

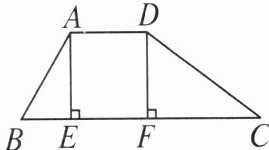
7. 为防水患,在水库上游修筑了防洪堤,如图,其截面为梯形。堤的上底 $ AD $ 和堤高 $ DF $ 都是 $ 6 $ m,其中 $ \angle B = \angle CDF $。
(1)求证：$ \triangle ABE \sim \triangle CDF $；
(2)如果 $ \frac{AE}{BE} = 2 $,求堤的下底 $ BC $ 的长。

答案：
(1)证明：在△ABE和△CDF中，∠AEB = ∠CFD = 90°，∠B = ∠CDF，
∴△ABE∽△CDF.
(2)解：
∵$\frac{AE}{BE}=2$，AE = DF = 6m，
∴$BE=\frac{1}{2}AE=3$m.
又△ABE∽△CDF，
∴$\frac{AE}{CF}=\frac{BE}{DF}$，
∴$CF=\frac{AE}{BE}·DF=2×6=12$(m).
易知AD = EF = 6m，
∴BC = BE + EF + FC = 3 + 6 + 12 = 21(m).

8. 如图,在一个长为 $ 40 $ m,宽为 $ 30 $ m 的长方形操场上,小明从点 $ A $ 出发,沿着 $ A \to B \to C $ 的路线以 $ 3 $ m/s 的速度跑向 $ C $ 地,当他出发 $ 4 $ s 后,小华有东西需要交给他,就从 $ A $ 地出发沿小明走的路线追赶。当小华跑到距 $ B $ 地 $ 2 \frac{2}{3} $ m 的 $ D $ 处时,他和小明在阳光下的影子恰好重叠在同一条直线上,此时,$ A $ 处有一根电线杆在阳光下的影子也恰好落在对角线 $ AC $ 上。
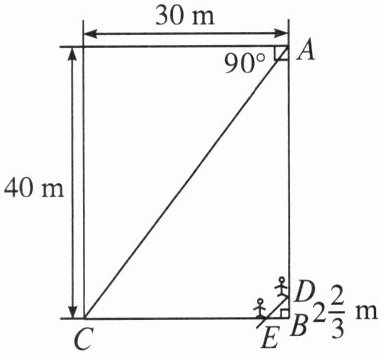
(1)求他们的影子重叠时,两人相距多少米($ DE $ 的长)；
(2)求小华追赶小明的速度是多少。(精确到 $ 0.1 $ m/s)

答案：
(1)由阳光与影子的性质，可知DE//AC，
∴∠BDE = ∠BAC，∠BED = ∠BCA.
∴△BDE∽△BAC，
∴$\frac{DE}{BD}=\frac{AC}{AB}$.
∵$AC=\sqrt{30^2+40^2}=50$(m)，$BD=\frac{8}{3}$m，AB = 40m，
∴$DE=\frac{10}{3}$m.
(2)$BE=\sqrt{DE^2 - BD^2}=2$m，小明到达E处所用的时间为$\frac{40 + 2}{3}=14$(s)，小华到达D处所用的时间为14 - 4 = 10(s)，小华追赶小明的速度为$(40-\frac{8}{3})÷10≈3.7$(m/s).