《2025年初中同步练习册九年级数学上册鲁教版54制山东科学技术出版社》

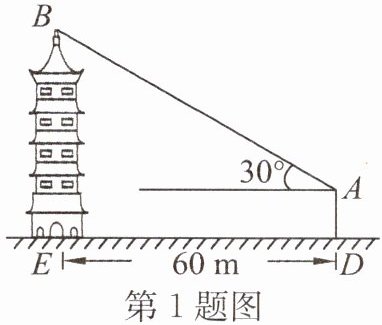
1. 小强和小明去测量古塔BE的高度。如图,他们在离古塔60m远的A处,用测角仪测得古塔顶的仰角为30°。已知测角仪高AD= 1.5m,则古塔BE的高为(B)

A.(20√{3} - 1.5)m
B.(20√{3} + 1.5)m
C.(31.5 - 2√{3})m
D.(28.5 + 3√{3})m

答案： B

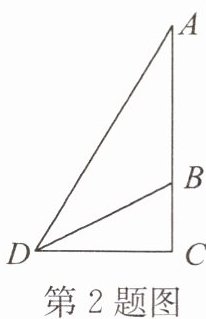
2. 如图,从D处测得塔顶A点和塔基B点的仰角分别为60°和30°。已知塔基高出地面20m(即BC为20m),则塔身AB的高为(C)

A.60m
B.40√{3}m
C.40m
D.20m

答案： C

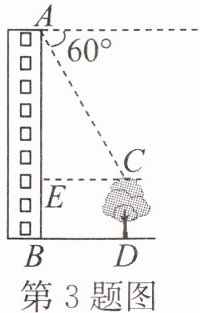
3. 如图,王师傅在楼顶上的点A处测得楼前一棵树CD的顶端C的俯角为60°,又知水平距离BD= 10m,楼高AB= 24m,则树CD的高为(A)

A.(24 - 10√{3})m

$B.(24 - \frac{10√{3}}{3})m$
C.(24 - 5√{3})m
D.9m

答案： A

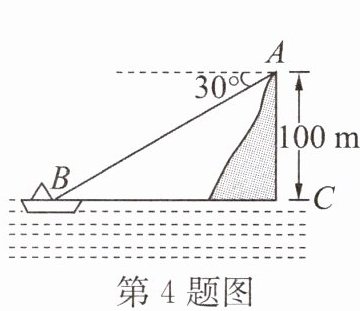
4. 如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,测得它的俯角为30°,则小船B与观测者间的水平距离BC= $100\sqrt{3}$m。

答案： $100\sqrt{3}$

例1 如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°。已知测角仪的高度是1.5m,请计算该建筑物的高度(取√{3} ≈ 1.732,结果精确到1m)。

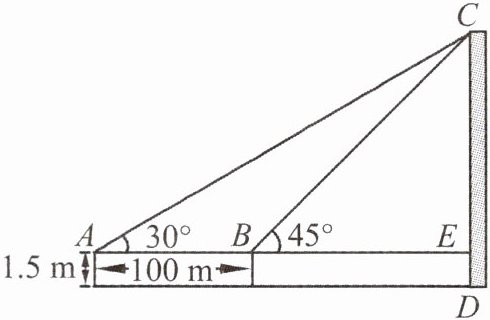
【点拨】分别在Rt△AEC与Rt△BEC中利用三角函数表示AE,BE,CE的关系,利用AE - BE = 100m求CE的长。

答案： 设CE = x m。
在Rt△BEC中，∠CBE = 45°，tan∠CBE = CE/BE，即tan45° = x/BE = 1，
∴BE = x m。
AE = AB + BE = 100 + x m。
在Rt△AEC中，∠CAE = 30°，tan∠CAE = CE/AE，即tan30° = x/(x + 100) = √3/3。
解得x = 50(√3 + 1) ≈ 50×(1.732 + 1) = 136.6 m。
CD = CE + ED = 136.6 + 1.5 = 138.1 ≈ 138 m。
答：该建筑物的高度约为138 m。