《2025年初中同步练习册九年级数学上册鲁教版54制山东科学技术出版社》

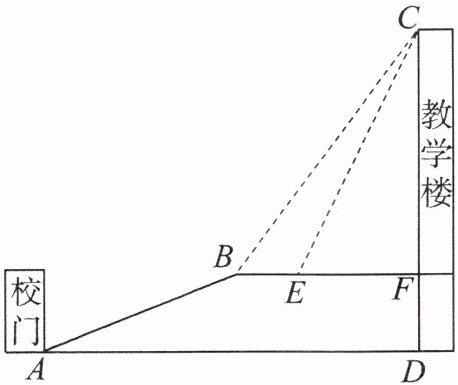
18. (9 分)某中学依山而建. 校门 $A$ 处有一斜坡 $AB$,其长度为 $13\mathrm{m}$. 在坡顶 $B$ 处看教学楼 $CF$ 的楼顶 $C$ 的仰角 $\angle CBF = 53^{\circ}$. 离 $B$ 点 $4\mathrm{m}$ 远的 $E$ 处有一花坛,在 $E$ 处看教学楼 $CF$ 的楼顶 $C$ 的仰角 $\angle CEF = 63.4^{\circ}$. 已知 $CF$ 的延长线交校门处的水平面于 $D$ 点,$FD = 5\mathrm{m}$.
(1)求斜坡 $AB$ 的坡度 $i$；
(2)试求 $DC$ 的长.(参考数据：$\tan 53^{\circ} \approx \frac{4}{3}$,$\tan 63.4^{\circ} \approx 2$)

答案：
解:
(1)如图,过点B作BG⊥AD于点G,则四边形BGDF是矩形.
∴BG=DF=5 m.
∵AB=13 m,
∴$AG=\sqrt{AB^2-BG^2}=\sqrt{13^2-5^2}=12(m)$,
∴AB的坡度$i=\frac{BG}{AG}=1:2.4$.
(2)在Rt△BCF中,$BF=\frac{CF}{\tan\angle CBF}\approx\frac{CF}{\frac{4}{3}}$.在Rt△CEF中,$EF=\frac{CF}{\tan\angle CEF}\approx\frac{CF}{2}$.
∵BE=4 m,
∴$BE=BF - EF\approx\frac{CF}{\frac{4}{3}}-\frac{CF}{2}=4(m)$,
∴CF≈16 m.
∴DC=CF+DF≈16+5=21(m).

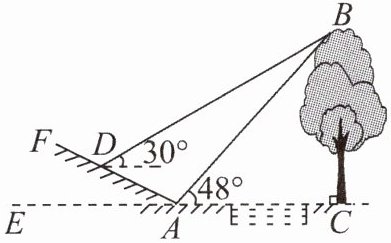
19. (9 分)如图,某数学活动小组要测量小河对岸大树 $BC$ 的高度. 他们先在斜坡上的 $D$ 处测得大树顶端 $B$ 的仰角是 $30^{\circ}$,再沿着斜坡走 $6\mathrm{m}$ 到达坡底 $A$ 处,在 $A$ 处测得大树顶端 $B$ 的仰角是 $48^{\circ}$. 若坡角 $\angle FAE = 30^{\circ}$,求大树 $BC$ 的高度.(结果保留整数. 参考数据：$\sin 48^{\circ} \approx 0.74$,$\cos 48^{\circ} \approx 0.67$,$\tan 48^{\circ} \approx 1.11$,$\sqrt{3} \approx 1.73$)

答案：
解:如图,过点D作DG⊥BC于点G,DH⊥CE于点H,则四边形DHCG为矩形. 故DG=CH,CG=DH.在Rt△AHD中,
∵$\angle DAH=30°$,AD=6 m,
∴DH=3 m,$AH=3\sqrt{3}$ m,
∴CG=3 m.设BC=x m.在Rt△ABC中,$AC\approx\frac{x}{1.11}$ m.
∴$DG\approx(3\sqrt{3}+\frac{x}{1.11})m$,BG=(x - 3)m.在Rt△BDG中,
∵$BG=DG\cdot\tan30°$,
∴$x - 3=(3\sqrt{3}+\frac{x}{1.11})×\frac{\sqrt{3}}{3}$.解得x≈13.
∴大树BC的高度约为13 m.