第103页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
9. 已知某网店专售一款休闲裤,其成本价为40元/条. 据市场调查发现,每月的销售量y与售价x的关系如下表:
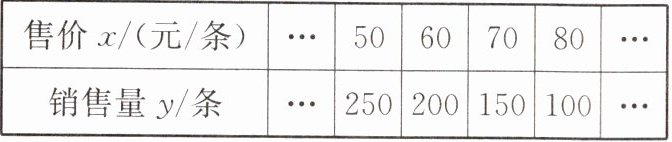
(1)直接写出y与x之间的函数关系式(不要求写出x的取值范围).
(2)若每月的利润为4000元,且让消费者得到最大的实惠,则售价应为多少元/条?
(3)设该网店每月获得的利润为w元,当售价定为多少元/条时,每月获得的利润最大? 最大利润是多少?

(1)直接写出y与x之间的函数关系式(不要求写出x的取值范围).
(2)若每月的利润为4000元,且让消费者得到最大的实惠,则售价应为多少元/条?
(3)设该网店每月获得的利润为w元,当售价定为多少元/条时,每月获得的利润最大? 最大利润是多少?
答案:
解:
(1)y=-5x+500.
(2)根据题意,得(x-40)(-5x+500)=4000.
整理得-5x²+700x-24000=0,
即x²-140x+4800=0.
解得x₁=60,x₂=80.
∵要让消费者得到最大的实惠,
∴售价应为60元/条.
(3)根据题意,得w=(x-40)(-5x+500)
=-5x²+700x-20000
=-5(x-70)²+4500.
∵a=-5<0,
∴当x=70时,w有最大值,为4500.
∴当售价定为70元/条时,每月获得的利润最大,最大利润是4500元.
(1)y=-5x+500.
(2)根据题意,得(x-40)(-5x+500)=4000.
整理得-5x²+700x-24000=0,
即x²-140x+4800=0.
解得x₁=60,x₂=80.
∵要让消费者得到最大的实惠,
∴售价应为60元/条.
(3)根据题意,得w=(x-40)(-5x+500)
=-5x²+700x-20000
=-5(x-70)²+4500.
∵a=-5<0,
∴当x=70时,w有最大值,为4500.
∴当售价定为70元/条时,每月获得的利润最大,最大利润是4500元.
1. 设某种礼炮的升空高度 $ h(m) $ 与飞行时间 $ t(s) $ 之间的函数关系式是 $ h = -(t - 4)^2 + 20 $.若此礼炮升空到最高处时引爆,则从升空到引爆需要的时间为(
A.$ 3 s $
B.$ 4 s $
C.$ 5 s $
D.$ 6 s $
B
)A.$ 3 s $
B.$ 4 s $
C.$ 5 s $
D.$ 6 s $
答案:
B
2. 设飞机着陆后滑行的距离 $ y(m) $ 与滑行时间 $ t(s) $ 之间的函数关系式是 $ y = 60t - \frac{3}{2}t^2 $.在飞机着陆滑行中,滑行最后的 $ 150 m $ 所用的时间是(
A.$ 10 s $
B.$ 20 s $
C.$ 30 s $
D.$ 10 s $ 或 $ 30 s $
A
)A.$ 10 s $
B.$ 20 s $
C.$ 30 s $
D.$ 10 s $ 或 $ 30 s $
答案:
A
3. 如图,一位运动员推铅球,铅球行进高度 $ y(m) $ 与水平距离 $ x(m) $ 之间的函数关系式是 $ y = -\frac{1}{12}x^2 + \frac{2}{3}x + \frac{5}{3} $,则此运动员把铅球推出的距离是(
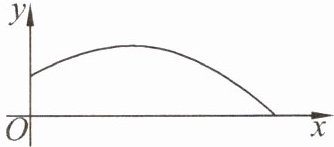
A.$ 12 m $
B.$ 10 m $
C.$ 3 m $
D.$ 4 m $
B
)
A.$ 12 m $
B.$ 10 m $
C.$ 3 m $
D.$ 4 m $
答案:
B
4. 一位运动员在距篮下 $ 4 m $ 处跳起投篮,球运行的路线是抛物线.当球运行的水平距离为 $ 2.5 m $ 时,达到最大高度 $ 3.5 m $,然后准确落入篮圈.如图,建立平面直角坐标系.已知篮圈中心到地面的距离为 $ 3.05 m $,该运动员身高 $ 1.9 m $.在这次跳投中,球在头顶上方 $ 0.25 m $ 处出手时,他跳离地面的高度是(
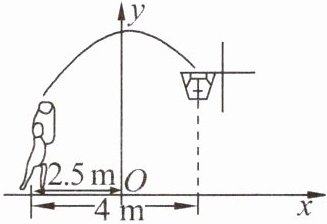
A
)
答案:
A
查看更多完整答案,请扫码查看


