《2025年名师学案九年级数学上册人教版》

8. 下列说法正确的是 (C)
A.相等的弦所对的弧相等
B.相等的圆心角所对的弧相等
C.等弧所对的弦相等
D.相等的弦所对的圆心角相等

答案： C

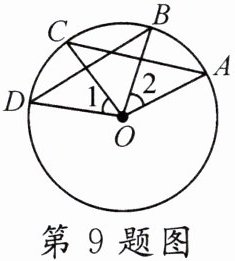
9. 如图,已知 A,B,C,D 是$\odot O$上的点,$∠1= ∠2$,则下列结论中正确的有 (D)
①$\widehat {AB}= \widehat {CD}$;②$\widehat {BD}= \widehat {AC}$;③$AC= BD$;④$∠BOD= ∠AOC.$

A.1个
B.2个
C.3个
D.4个

答案： D

10.【易错题】如图,在$\odot O$中,$\widehat {AB}= 2\widehat {CD}$,则下列结论正确的是 (C)
A.$AB＞2CD$
B.$AB= 2CD$
C.$AB＜2CD$
D.以上都不对
【点拨】取$\widehat {AB}$的中点 P,连接 PA,PB,结合已知条件可证$\widehat {PA}= \widehat {PB}= \widehat {CD}$,从而得到$PA= PB= CD$,再利用$\triangle PAB$的三边关系解答.

答案： C

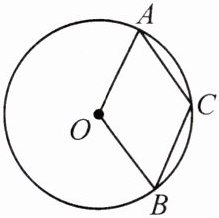
11.【教材 P90 习题 T13 变式】如图,A,B 是半径为 4 的$\odot O$上的两点.若$∠AOB= 120^{\circ }$,C 是$\widehat {AB}$的中点,则四边形 AOBC 是菱形,它的周长等于16.

答案： 菱形 16

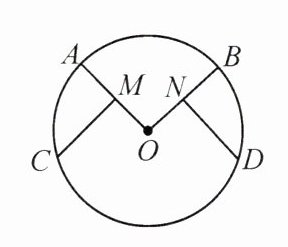
12.【教材 P123 复习题 T2 变式】如图,在$\odot O$中,$CM⊥OA$于点 M,$DN⊥OB$于点 N,且$AM= BN$. 求证:$\widehat {AC}= \widehat {BD}.$

答案： 证明:连接OC,OD.
∵OA=OB,AM=BN,
∴OA-AM=OB-BN.即OM=ON.
∵CM⊥OA,DN⊥OB,
∴∠CMO=∠DNO=90°.又
∵OC=OD,
∴Rt△COM≌Rt△DON.
∴∠COM=∠DON.
∴$\overset{\frown}{AC}=\overset{\frown}{BD}$.

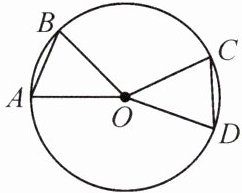
13.【新课标·作图能力】如图,A,B,C,D 都在$\odot O$上,$∠AOB+∠COD= 90^{\circ }.$
(1)将$\triangle COD$绕点 O 逆时针旋转得到$\triangle BOE$,使 OC 与 OB 重合,画出旋转后的图形;
(2)在(1)的条件下,求$∠ABE$的度数;
(3)若$AB= 2,CD= \sqrt {2}$,求$\odot O$的半径长.

答案：
(1)如图,△BOE即为所求;
(2)
∵∠AOB+∠COD=90°,由旋转知∠BOE=∠COD,
∴∠AOE=∠AOB+∠BOE=90°.
∵OA=OB=OE,
∴∠OAB=∠OBA,∠OBE=∠OEB.
∵∠OAB+∠OBA+∠OBE+∠OEB+∠AOE=360°,
∴2∠ABE+90°=360°.
∴∠ABE=(360°-90°)÷2=135°;
(3)如图,连接AE,过点E作EF⊥AB于点F,
∴∠EBF=45°.
∵BE=CD=$\sqrt{2}$,
∴EF=BF=1.
∴AF=AB+BF=3.
∴AE=$\sqrt{3^{2}+1^{2}}=\sqrt{10}$.在Rt△AOE中,OA²+OE²=AE²,
∴2OA²=($\sqrt{10}$)².解得OA=$\sqrt{5}$.
∴⊙O的半径长为$\sqrt{5}$.