《2025年名师学案九年级数学上册人教版》

6.【教材P52习题T3变式】某一型号飞机着陆后滑行的距离y(m)与滑行时间x(s)之间的函数关系式是$y= 40x-2x^{2}$,则该型号飞机着陆后需滑行200m才能停下来。

答案： 200

7.【新情境·“大课间”】为促进中学生全面发展,培养良好体质,某班同学在“大课间”开展“集体跳绳”运动。跳绳时,绳甩到最高处时的形状是抛物线$y= ax^{2}+bx+c$的部分图象。以点O为原点建立如图所示的平面直角坐标系,若摇绳的两人之间间距为6米,摇绳时两人手离地面均为$\frac {9}{10}$米。已知小丽身高1.575米,在距离摇绳者A的水平距离1.5米处,绳子刚好经过她的头顶。
(1)图中抛物线的解析式是____$y=-0.1x^{2}+0.6x+0.9$；
(2)龙老师身高1.82米,请问他适合参加本次运动吗？说明理由；
解:$\because -0.1＜0$,开口向下,$\therefore$当$x=3$时,有最大值$1.8$.$\because 1.8\ \text{m}＜1.82\ \text{m}$,$\therefore$他不适合参加本次运动;
(3)若多人进入跳绳区齐跳,且大家身高均为1.7米,要求相邻两人之间间距至少为0.6米,试计算最多可供几人齐跳？
解:当$y=1.7$时.$-0.1x^{2}+0.6x+0.9=1.7$.解得$x_{1}=2$,$x_{2}=4$.$\therefore 4-2=2$(米).$\because$相邻两人之间间距至少为$0.6$米$\therefore$间距个数为:$2÷0.6=3\dfrac{1}{3}$.答:最多可供4人齐跳.

答案：
(1)$y=-0.1x^{2}+0.6x+0.9$ 解:
(2)$\because -0.1＜0$,开口向下,$\therefore$当$x=3$时,有最大值$1.8$.$\because 1.8\ \text{m}＜1.82\ \text{m}$,$\therefore$他不适合参加本次运动;
(3)当$y=1.7$时.$-0.1x^{2}+0.6x+0.9=1.7$.解得$x_{1}=2$,$x_{2}=4$.$\therefore 4-2=2$(米).$\because$相邻两人之间间距至少为$0.6$米$\therefore$间距个数为:$2÷0.6=3\dfrac{1}{3}$.答:最多可供4人齐跳.

8.(中考·河南)小林同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析。
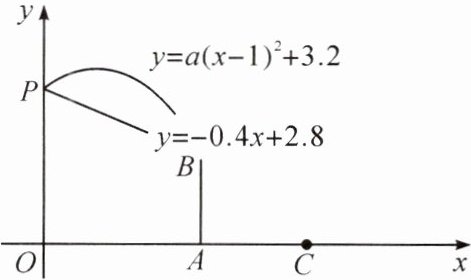
如图,在平面直角坐标系中,点A,C在x轴上,球网AB与y轴的水平距离$OA= 3m$,$CA= 2m$,击球点P在y轴上。若选择扣球,羽毛球的飞行高度y(m)与水平距离x(m)近似满足一次函数关系$y= -0.4x+2.8$；若选择吊球,羽毛球的飞行高度y(m)与水平距离x(m)近似满足二次函数关系$y= a(x-1)^{2}+3.2$。
(1)点P的坐标是(0,2.8),a的值是-0.4；
(2)小林分析发现,上面两种击球方式均能使球过网,要使球的落地点到C点的距离更近,请通过计算判断应选择哪种击球方式。

解:
由题意可知点$C$的坐标是$(5,0)$.在$y=-0.4x+2.8$中,令$y=0$得$x=7$.在$y=-0.4(x-1)^{2}+3.2$中,令$y=0$,得$x=-2\sqrt{2}+1$(舍去)或$x=2\sqrt{2}+1\approx3.82$.$\because|7-5|＞|3.82-5|$,$\therefore$选择吊球方式,球的落地点到$C$的距离更近.

答案：
(1)$(0,2.8)$ $-0.4$ 解:
(2)由题意可知点$C$的坐标是$(5,0)$.在$y=-0.4x+2.8$中,令$y=0$得$x=7$.在$y=-0.4(x-1)^{2}+3.2$中,令$y=0$,得$x=-2\sqrt{2}+1$(舍去)或$x=2\sqrt{2}+1\approx3.82$.$\because|7-5|＞|3.82-5|$,$\therefore$选择吊球方式,球的落地点到$C$的距离更近.