《2025年名师学案九年级数学上册人教版》

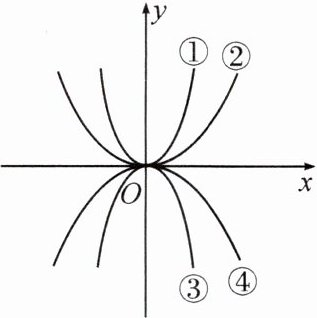
7. 【数形结合思想】如图,四条抛物线所对应的函数解析式分别为：①$y= ax^{2}$；②$y= bx^{2}$；③$y= cx^{2}$；④$y= dx^{2}$。比较$a,b,c,d$的大小,用“＞”连接为a＞b＞d＞c。

答案： a＞b＞d＞c

8. 关于二次函数$y= 3x^{2}$,给出下列说法：
①图象开口向下,对称轴是$y$轴；
②当$x＞10$时,$y随x$的增大而增大；
③当$-1＜x＜2$时,$3＜y＜12$；
④若$(m,n),(p,n)$是该抛物线上的两个不同的点,则$m+p= 0$。
其中说法正确的有②④(填序号)。

答案： ②④

9. 如图,抛物线$y= ax^{2}经过点A(-2,-8)$。
(1)此抛物线的解析式是y=−2x²；
(2)点$B(-1,-4)$不在(填“在”或“不在”)是否在此抛物线上；
(3)点$P(m,-6)$在此抛物线第三象限的图象上,过点$P作PQ// x轴交抛物线于另一点Q$,求$\triangle POQ$的面积。
解:
∵点P在此抛物线第三象限图象上,
∴−6=−2m²,
∴m=±$\sqrt{3}$.
∴P(−$\sqrt{3}$,−6)
∵PQ//x轴,
∴Q($\sqrt{3}$,−6).
∴PQ=2$\sqrt{3}$
∴S△POQ=$\frac{1}{2}$×2$\sqrt{3}$×6=6$\sqrt{3}$.

答案：
(1)y=−2x²　
(2)不在 解:
(3)
∵点P在此抛物线第三象限图象上,
∴−6=−2m²,
∴m=±$\sqrt{3}$.
∴P(−$\sqrt{3}$,−6)
∵PQ//x轴,
∴Q($\sqrt{3}$,−6).
∴PQ=2$\sqrt{3}$
∴S△POQ=$\frac{1}{2}$×2$\sqrt{3}$×6=6$\sqrt{3}$.

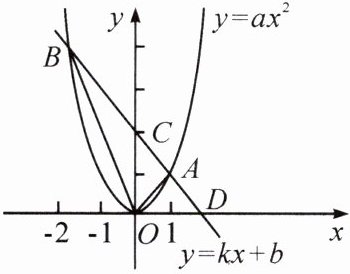
10. 如图,一次函数$y= kx+b的图象与二次函数y= ax^{2}图象交于点A(1,m)和B(-2,4)$,与$y轴交于点C$,与$x轴交于点D$。
(1)$a= $1,$b= $2,$k= $−1；
(2)求$\triangle AOB$的面积；
(3)点$P$是抛物线上一点,且$\triangle POD的面积与\triangle AOB$的面积相等,求点$P$的坐标。

(2)令y=−x+2中x=0,则y=2,
∴C(0,2),
∵S△AOC=$\frac{1}{2}$OC·|1|=$\frac{1}{2}$×2×1=1,S△BOC=$\frac{1}{2}$OC·|−2|=$\frac{1}{2}$×2×2=2,
∴S△AOB=S△AOC+S△BOC=1+2=3.
(3)设P(x,y),由题意知y＞0.令y=−x+2=0,得x=2,
∴D(2,0).
∵S△POD=S△AOB=3,
∴$\frac{1}{2}$·OD·|y|=3,即$\frac{1}{2}$×2·|y|=3.
∴y=±3.
∵y＞0,
∴y=3.
∴x²=3,解得x=±$\sqrt{3}$.
∴P($\sqrt{3}$,3)或(−$\sqrt{3}$,3).

答案：
(1)1　2　−1　解:
(2)令y=−x+2中x=0,则y=2,
∴C(0,2),
∵S△AOC=$\frac{1}{2}$OC·|1|=$\frac{1}{2}$×2×1=1,S△BOC=$\frac{1}{2}$OC·|−2|=$\frac{1}{2}$×2×2=2,
∴S△AOB=S△AOC+S△BOC=1+2=3.
(3)设P(x,y),由题意知y＞0.令y=−x+2=0,得x=2,
∴D(2,0).
∵S△POD=S△AOB=3,
∴$\frac{1}{2}$·OD·|y|=3,即$\frac{1}{2}$×2·|y|=3.
∴y=±3.
∵y＞0,
∴y=3.
∴x²=3,解得x=±$\sqrt{3}$.
∴P($\sqrt{3}$,3)或(−$\sqrt{3}$,3).