《2025年名师学案九年级数学上册人教版》

1.【感知】如图①,△ABC和△ADE都是等腰直角三角形,∠BAC= ∠DAE= 90°,点B在线段AD上,点C在线段AE上,我们很容易得到BD= CE,不需证明.
【探究】如图②,将△ADE绕点A逆时针旋转α(0＜α＜90°),连接BD和CE,此时BD= CE是否依然成立?若成立,写出证明过程;若不成立,说明理由.
【应用】如图③,当△ADE绕点A逆时针旋转,使得点D落在BC的延长线上,连接CE.
①∠ACE的度数为45°;
②若AB= AC= 2√2,CD= 2,求线段DE的长.∵AB=AC=2√2,
∴BC=√(AB²+AC²)=4.
∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE.
∴BD=CE.
∴∠ACE=∠ABD=45°.
∴∠BCE=∠ACB+∠ACE=90°.
∴BC+CD=BD=CE=4+2=6.
∴DE=√(CE²+CD²)=√(6²+2²)=2√10.

答案： 1.解:【探究】BD=CE依然成立.证明:
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE.
∵将△ADE绕点A逆时针旋转α,
∴∠BAD=∠CAE.
∴△ABD≌△ACE.
∴BD=CE;【应用】①45° ②
∵AB=AC=2√2,
∴BC=√(AB²+AC²)=4.
∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE.
∴BD=CE.
∴∠ACE=∠ABD=45°.
∴∠BCE=∠ACB+∠ACE=90°.
∴BC+CD=BD=CE=4+2=6.
∴DE=√(CE²+CD²)=√(6²+2²)=2√10.id:3
answer:2.解:
(1)AD=CF.理由如下:在正方形ABCO和正方形ODEF中,AO=CO,OD=OF,∠AOC=∠DOF=90°,
∴∠AOC+∠COD=∠DOF+∠COD,即∠AOD=∠COF.
∴△AOD≌△COF(SAS).
∴AD=CF;
(2)√17id:7
answer:3.
(1)证明:
∵将△ADF绕点A顺时针旋转90°得到△ABG,
∴△ADF≌△ABG.
∴DF=GB,AG=AF,∠DAF=∠BAG,∠D=∠ABG=90°.
∴∠ABG+∠ABC=180°,即点G,B,E三点共线.
∵∠DAB=90°,∠EAF=45°,
∴∠DAF+∠EAB=45°.
∴∠BAG+∠EAB=45°.即∠EAF=∠EAG.
∴△EAG≌△EAF.
∴EF=GE=GB+BE=DF+BE;
(2)2id:11
answer:4.√5id:15answer:5.解:EF=BE+DF,理由如下:
∵∠BAD=120°,∠C=60°,
∴∠ABC+∠D=360°-120°-60°=180°.
∵把△ADF绕点A顺时针旋转得△ABM,
∴△ABM≌△ADF,∠MAF=∠DAB=120°.
∴BM=DF,∠ABM=∠D,AM=AF.
∴∠ABM+∠ABC=180°,即点M,B,E共线.
∵∠EAF=60°,
∴∠EAM=120°-60°=60°=∠EAF.又
∵AM=AF,AE=AE,
∴△EAM≌△EAF.
∴EF=EM=BM+BE=DF+BE.id:17
answer:6.解:由旋转的性质可知,AB=AE,∠BAE=90°,
∴△ABE是等腰直角三角形.
∵△ACD是等腰直角三角形,
∴AC=AD.
∴∠BAE=∠CAD=90°.
∴∠BAE+∠EAD=∠CAD+∠EAD,即∠BAD=∠EAC.
∴△ABD≌△AEC(SAS).
∴BD=EC.
∵AB=AE=√2,
∴BE=√(AB²+AE²)=2.
∵∠ABC=45°,
∴∠EBC=∠EBA+∠ABC=90°.
∴BD=EC=√(BE²+BC²)=√(2²+4²)=2√5.

2.小明在数学活动课上,将边长为√2和3的两个正方形放置在直线l上,如图1,他连接AD,CF,经测量发现AD= CF.

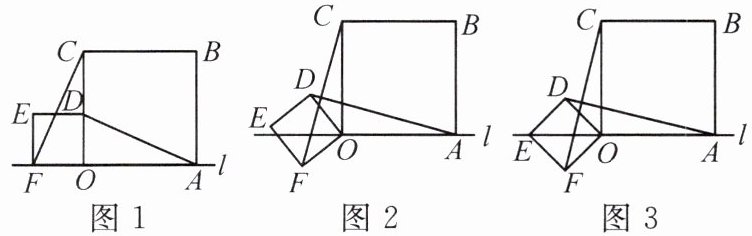
(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明理由;
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,则CF的长为______√17或√5.

答案：
(1)AD=CF。证明：
∵四边形ABCO和四边形ODEF是正方形，
∴AO=CO，OD=OF，∠AOC=∠DOF=90°，
∴∠AOC+∠COD=∠DOF+∠COD，即∠AOD=∠COF，在△AOD和△COF中，AO=CO，∠AOD=∠COF，OD=OF，
∴△AOD≌△COF(SAS)，
∴AD=CF。
(2)√17或√5。