《2025年名师学案九年级数学上册人教版》

1. 当$x= $1时,二次函数$y= -x^{2}+2x+3$有最大值,为4.

答案： 1 大 4

2. 已知二次函数$y= x^{2}-4x+c$的最小值是0,则c的值是4.

答案： 4

3. 当$-1\leqslant x\leqslant 3$时,二次函数$y= x^{2}-4x-5$有最大值是0,最小值是-9.

答案： 0 -9

4. 如图,假设篱笆(虚线部分)的长度为16m,则所围成矩形ABCD的最大面积是(C)
A.$60m^{2}$
B.$63m^{2}$
C.$64m^{2}$
D.$66m^{2}$

答案： C

5. 【教材P52习题T4变式】一个直角三角形两条直角边之和是20cm,则这个直角三角形的最大面积是50$cm^{2}$.

答案： 50

6. 如图,已知$□ ABCD$的周长为8cm,$\angle B= 30^{\circ}$,若边长$AB= xcm$,过点A作$AE\perp BC$于点E.

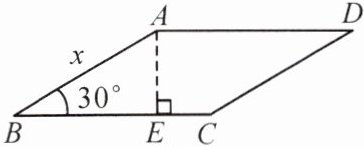
(1)$AE= $$\dfrac{1}{2}x$(用含x的代数式表示)；
(2)$□ ABCD的面积y(cm^{2})$与x之间的函数解析式为$y=-\dfrac{1}{2}x^{2}+2x$,自变量x的取值范围为0＜x＜4；
(3)当x取2时,y的值最大,最大值为2.

答案：
(1)$\dfrac{1}{2}x$
(2)$y=-\dfrac{1}{2}x^{2}+2x$ 0＜x＜4
(3)2 2

7. 某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体,抽屉底面周长为180cm,高为20cm.请通过计算说明,当抽屉底面的宽$x(cm)$为何值时,抽屉的体积$y(cm^{3})$最大?最大为多少?(材质及其厚度等忽略不计)

答案： 解:依题意,得$y=20x(90-x)$.即$y=-20(x^{2}-90x)=-20(x-45)^{2}+40500$.$\because a=-20＜0$,抛物线开口向下,$\therefore$当$x=45$时,$y_{\text{最大}}=40500$.答:当抽屉底面的宽x为45cm时,体积最大,最大值为40500$\unit{cm^{3}}$.

8. (教材P49“探究1”改编) 一材多题
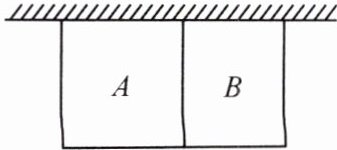
某学校为美化学校环境,打造绿色校园,决定用篱笆围成一个一面靠墙(墙足够长)的矩形花园,用一道篱笆把花园分为A,B两块(如图所示),花园里种满牡丹和芍药.学校已定购篱笆120m.
(1)设与墙垂直的边是xm,则与墙平行的边长为(120-3x)m,所围成矩形花园的面积$S(m^{2})与x(m)$之间的函数关系式是$S=x(120-3x)$；
(2)若围成花园的面积是$900m^{2}$,则x的值是10或30；
(3)设计一种方案,使所围成花园的面积最大.由(1)知,$S=x(120-3x)=-3x^{2}+120x$.$\because -3＜0$,$\therefore$当$x=-\dfrac{120}{-6}=20$时,S取最大值1200.$\therefore 120-3x=120-3×20=60$.答:垂直于墙的边为20米,平行于墙的边为60米,花园面积最大为1200平方米.

答案：
(1)(120-3x) $S=x(120-3x)$
(2)10或30 解:
(3)由
(1)知,$S=x(120-3x)=-3x^{2}+120x$.$\because -3＜0$,$\therefore$当$x=-\dfrac{120}{-6}=20$时,S取最大值1200.$\therefore 120-3x=120-3×20=60$.答:垂直于墙的边为20米,平行于墙的边为60米,花园面积最大为1200平方米.