第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
6. 一个两位数等于它个位上的数的平方,且个位上的数比十位上的数大3,求这个两位数.
答案:
解:设这个两位数十位上的数为x,则个位上的数为$x+3$.由题意,得$10x+x+3=(x+3)^{2}$.解得$x_{1}=2$,$x_{2}=3$.当$x=2$时,$x+3=5$;当$x=3$时,$x+3=6$.$\therefore$这个两位数是25或36.
7. 某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了10条航线,则这个航空公司一共有飞机场
5
个.
答案:
5
8. 某校团体操表演队伍有6行8列,后又增加了51人,使得团体操表演队伍增加的行、列数相同,则增加了
3
行.
答案:
3
9. 在2025年5月的日历上用一个方框圈出4个数(如图所示),若圈出的四个数中,最小数与最大数的乘积为65,求这个最小数(请用方程知识解答).


答案:
解:设这个最小数为x,则最大数为$(x+8)$.由题意,得$x(x+8)=65$.整理,得$x^{2}+8x-65=0$.解得$x_{1}=5$,$x_{2}=-13$(不合题意,舍去).答:这个最小数为5.
10. 一个三位数,百位数字比个位数字大1,十位数字比个位数字小3. 已知这个三位数比百位数字和个位数字的积的20倍大25,求这个三位数. 设这个三位数的个位数字为x.
(1)该三位数的百位数字为
(2)求该三位数.
(1)该三位数的百位数字为
(x+1)
,十位数字为(x-3)
;(用含x的代数式表示)(2)求该三位数.
解:由题意,得100(x+1)+10(x-3)+x=20x(x+1)+25.整理,得20x²-91x-45=0.解得x=5(负值已舍去),则x+1=6,x-3=2,∴该三位数是625.
答案:
(1)$(x+1)$ $(x-3)$
(2)解:由题意,得$100(x+1)+10(x-3)+x=20x(x+1)+25$.整理,得$20x^{2}-91x-45=0$.解得$x=5$(负值已舍去),则$x+1=6$,$x-3=2$,$\therefore$该三位数是625.
(1)$(x+1)$ $(x-3)$
(2)解:由题意,得$100(x+1)+10(x-3)+x=20x(x+1)+25$.整理,得$20x^{2}-91x-45=0$.解得$x=5$(负值已舍去),则$x+1=6$,$x-3=2$,$\therefore$该三位数是625.
11. (教材P4习题T6改编)
【新课标·传统文化】春节期间,九(1)班全体同学通过打电话的方式互相拜年,如果该班共有48名同学,若每两名同学之间仅通过一次电话,那么全班同学共通过多少次电话呢? 我们可以用下面的方式来解决问题:用点$A_{1},A_{2},A_{3},…,A_{48}$分别表示第1名同学、第2名同学、第3名同学……第48名同学,把该班级人数x与通电话次数y之间的关系用如图模型表示:
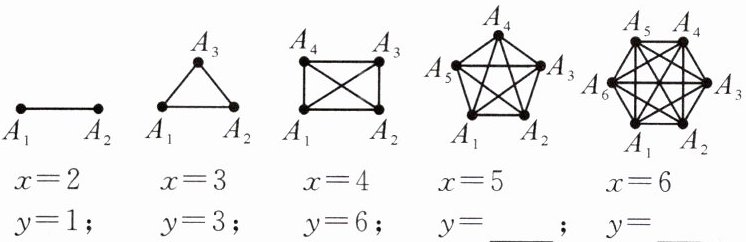
(1)第四个图中y的值为
(2)通过探索发现,通电话次数y与该班级人数x之间的关系式为
(3)若九(1)班全体女生相互之间共通话190次,则该班共有
【新课标·传统文化】春节期间,九(1)班全体同学通过打电话的方式互相拜年,如果该班共有48名同学,若每两名同学之间仅通过一次电话,那么全班同学共通过多少次电话呢? 我们可以用下面的方式来解决问题:用点$A_{1},A_{2},A_{3},…,A_{48}$分别表示第1名同学、第2名同学、第3名同学……第48名同学,把该班级人数x与通电话次数y之间的关系用如图模型表示:

(1)第四个图中y的值为
10
,第五个图中y的值为15
;(2)通过探索发现,通电话次数y与该班级人数x之间的关系式为
$y=\frac{1}{2}x(x-1)$
,当x= 48时,对应的y=1128
;(3)若九(1)班全体女生相互之间共通话190次,则该班共有
20
名女生.
答案:
(1)10 15
(2)$y=\frac{1}{2}x(x-1)$ 1128
(3)20
(1)10 15
(2)$y=\frac{1}{2}x(x-1)$ 1128
(3)20
查看更多完整答案,请扫码查看


