《2025年名师学案九年级数学上册人教版》

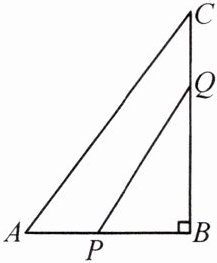
7. 如图,在$\triangle ABC$中,$∠B= 90^{\circ },AB= 5cm$,$BC= 7cm$. 点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果点P,Q分别从点A,B同时出发,那么1秒后,$\triangle PBQ的面积等于4cm^{2}$；
(2)如果点P,Q分别从点A,B同时出发,$\triangle PBQ的面积能否等于7cm^{2}$？

(2)设 x s后,△PBQ 的面积是7 cm².由题意,得$\frac{1}{2}\cdot 2x(5-x)=7$,即$x^{2}-5x+7=0$.$\Delta=(-5)^{2}-4×7＜0$,$\therefore$此方程无实数根.$\therefore\triangle PBQ$的面积不能等于7 cm².

答案：
(1)1 解:
(2)设 x s后,△PBQ 的面积是7 cm².由题意,得$\frac{1}{2}\cdot 2x(5-x)=7$,即$x^{2}-5x+7=0$.$\Delta=(-5)^{2}-4×7＜0$,$\therefore$此方程无实数根.$\therefore\triangle PBQ$的面积不能等于7 cm².

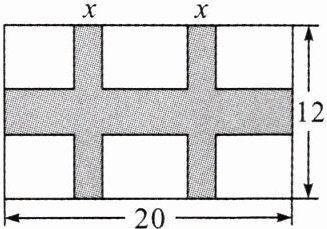
8. 【教材P22习题T9变式】如图,有一幅长20cm、宽12cm的长方形图案,其中有一横两竖的彩条,横、竖彩条的宽度比为$3:2$. 设竖彩条的宽度为xcm,若图案中三条彩条所占面积是图案面积的$\frac {2}{5}$,求横、竖彩条的宽度.

答案： 解:由题意知,横彩条宽度为$\frac{3}{2}$x cm,列方程,得$(20-2x)(12-\frac{3}{2}x)=20×12×(1-\frac{2}{5})$.解得$x_{1}=2,x_{2}=16$(舍去).$\therefore x=2,\frac{3}{2}x=3$.答:竖彩条宽 2 cm,横彩条宽 3 cm.

03 素养练
学科素养培育
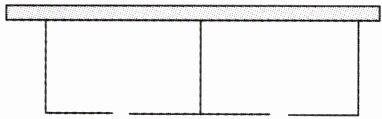
9. 如图,要利用一面足够长的墙为一边,其余三边用总长33m的围栏建两个面积相同的矩形生态园,为了出入方便,每个生态园在平行于墙的一边各留了一个宽1.5m的门,能够建生态园的场地垂直于墙的一边长不超过6m(围栏宽忽略不计).
(1)每个生态园的面积为$48m^{2}$,求每个生态园与墙平行的一边的长；
(2)每个生态园的面积能不能达到$108m^{2}$？若不能,请说明理由.

答案： 解:
(1)设与墙垂直的边长 x m,则与墙平行的边长(33-3x+3)m,由题意,得(33-3x+3)·x=48×2.解得$x_{1}=4,x_{2}=8$.$\because x\leq6$,$\therefore x=4$.当 x=4 时,36-3x=24,24÷2=12.答:每个生态园与墙平行的一边的长是 12 m.
(2)不能,理由如下:与设墙垂直的边长为 y m,由题意,得(33-3y+3)·y=108×2.化简整理,得$y^{2}-12y+72=0$.$\Delta=(-12)^{2}-4×72＜0$.$\therefore$此方程无实数根,$\therefore$不能围成.