《2025年名师学案九年级数学上册人教版》

6. 【新情境·科技助残】(2024·烟台)每年5月的第三个星期日为全国助残日,今年的主题是“科技助残,共享美好生活”. 康宁公司新研发了一批便携式轮椅,计划在该月销售. 根据市场调查,每辆轮椅盈利200元时,每天可售出60辆；单价每降低10元,每天可多售出4辆. 公司决定在成本不变的情况下降价销售,但每辆轮椅的利润不低于180元. 设每辆轮椅降价$x$元,每天的销售利润为$y$元.
(1)求$y与x$的函数关系式；每辆轮椅降价多少元时,每天的销售利润最大？最大利润为多少元？
(2)全国助残日当天,公司共获得销售利润12160元,请问这天售出了多少辆轮椅？

答案： 解:
(1)$ y=(200-x)\left(60+4×\frac{x}{10}\right)=-0.4x^{2}+20x+12000=-0.4(x^{2}-50x+625)+12250=-0.4(x-25)^{2}+12250 $.
∵$ 200-x\geqslant180 $,
∴$ x\leqslant20 $.
∵$ a=-5＜0 $,抛物线开口向下,对称轴是直线 $ x=25 $,$ x\leqslant20 $ 时,$ y $ 随 $ x $ 的增大而增大,
∴当 $ x=20 $ 时,利润最大,最大利润为:$ -0.4(20-25)^{2}+12250=12240 $(元).答:$ y $ 与 $ x $ 的函数关系式为:$ y=-0.4x^{2}+20x+12000 $;每辆轮椅降价 20 元时,每天的销售利润最大,最大利润为 12240 元;
(2)$ 12160=-0.4(x-25)^{2}+12250 $.解得 $ x_{1}=40 $(不合题意,舍去),$ x_{2}=10 $.
∴售出轮椅的辆数为:$ 60+4×\frac{10}{10}=64 $(辆).答:这天售出了 64 辆轮椅.

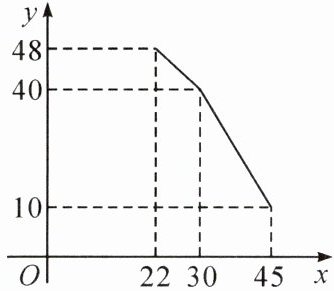
7. 某景区旅游商店以20元/kg的价格采购一款旅游食品加工后出售,销售价格不低于22元/kg,不高于45元/kg. 经市场调查发现每天的销售量$y$(kg)与销售价格$x$(元/kg)之间的函数关系如图所示.
(1)直接写出$y关于x$的函数表达式；
(2)当销售价格定为多少时,该商店销售这款食品每天获得的销售利润最大？最大销售利润是多少？[销售利润$=$(销售价格$-$采购价格)$×$销售量]

答案： 解:
(1)$ y $ 与 $ x $ 的函数表达式为:$ y=\begin{cases} -x+70(22\leqslant x\leqslant30) \\ -2x+100(30＜x\leqslant45) \end{cases} $;
(2)设利润为 $ w $ 元,当 $ 22\leqslant x\leqslant30 $ 时,$ w=(x-20)(-x+70)=-x^{2}+90x-1400=-(x-45)^{2}+625 $.
∵在 $ 22\leqslant x\leqslant30 $ 范围内,$ w $ 随着 $ x $ 的增大而增大,
∴当 $ x=30 $ 时,$ w $ 取得最大值为 400;当 $ 30＜x\leqslant45 $ 时,$ w=(x-20)(-2x+100)=-2x^{2}+140x-2000=-2(x-35)^{2}+450 $.当 $ x=35 $ 时,$ w $ 取得最大值为 450.
∵$ 450＞400 $,
∴当销售价格为 35 元/kg 时,每天的利润最大为 450 元.