《2025年综合应用创新题典中点九年级数学上册北师大版》

10. 如图所示的网格中,$\triangle ABC$的位似图形是______△NMP．

答案： △NMP

11. 如图,$\triangle ABC与\triangle DEF$是位似图形,位似中心为点$O$,且$OD= 3OA$,若$\triangle ABC$的面积为3,则阴影部分的面积是______24．

答案： 24 [点拨]
∵OD=3OA，
∴$\frac{OA}{OD}=\frac{1}{3}$.
易知$\frac{AB}{DE}=\frac{OA}{OD}=\frac{1}{3}$.
∴$\frac{S_{\triangle ABC}}{S_{\triangle DEF}}=(\frac{AB}{DE})^{2}=(\frac{1}{3})^{2}=\frac{1}{9}$.
∵△ABC的面积为3，
∴△DEF的面积为27.
∴阴影部分的面积是27−3=24.

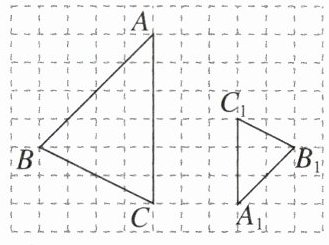
12. [2023济南历下区一模] 如图,在$8× 11$的网格图中,$\triangle ABC与\triangle A_1B_1C_1$是位似图形．
(1)在网格图中建立平面直角坐标系,使得点$A的坐标为(-1,6)$,点$C_1的坐标为(2,3)$,写出点$B$的坐标；
(2)以点$A$为位似中心,在网格图中作$\triangle AB_2C_2$,使$\triangle AB_2C_2和\triangle ABC$位似,且相似比为$1:2$；
(3)在图上标出$\triangle ABC与\triangle A_1B_1C_1的位似中心P$,并写出点$P$的坐标．

答案：
[解]
(1)坐标系如图，则点B的坐标为(−5,2).
(2)如图，△AB₂C₂为所作三角形.
(3)如图，点P为所作，点P的坐标为(1,2).
　　　　　　

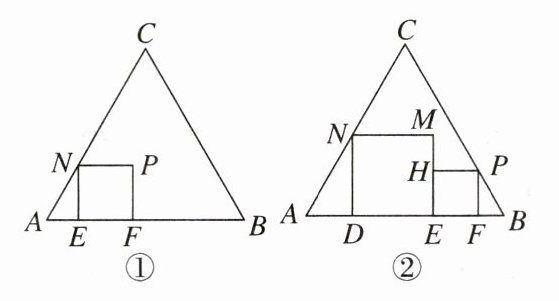
13. [2024北京西城区月考] 如图,正三角形$ABC的边长为3+\sqrt{3}$．
(1)如图①,正方形$EFPN的顶点E$,$F在边AB$上,顶点$N在边AC$上,在正三角形$ABC$及其内部,以点$A$为位似中心,作正方形$EFPN的位似正方形E'F'P'N'$,且使正方形$E'F'P'N'$的面积最大(不要求写作法)；
(2)求(1)中作出的正方形$E'F'P'N'$的边长；
(3)如图②,在正三角形$ABC中放入正方形DEMN和正方形EFPH$,使得$DE$,$EF在边AB$上,点$P$,$N分别在边CB$,$CA$上,求这两个正方形面积和的最大值和最小值,并说明理由．

答案：
[解]
(1)如图①，正方形E'F'P'N'即为所求.
　　　　　
(2)如图①，设正方形E'F'P'N'的边长为x.
∵△ABC为正三角形，
∴易得$AE'=BF'=\frac{\sqrt{3}}{3}x$.
∵E'F'+AE'+BF'=AB，
∴$x+\frac{\sqrt{3}}{3}x+\frac{\sqrt{3}}{3}x=3+\sqrt{3}$.
∴$x=\frac{9+3\sqrt{3}}{2\sqrt{3}+3}$，即$x=3\sqrt{3}−3$.
∴正方形E'F'P'N'的边长为$3\sqrt{3}−3$.
(3)这两个正方形面积和的最大值是$99−54\sqrt{3}$，最小值是$\frac{9}{2}$.理由如下：
如图②，连接NE，EP，PN，则∠NEP=90°.
设正方形DEMN、正方形EFPH的边长分别为m，n(m≥n)，它们的面积和为S，则$NE=\sqrt{2}m$，$PE=\sqrt{2}n$，S=m²+n²，
∴PN²=NE²+PE²=2m²+2n²=2(m²+n²).
∴$S=m^{2}+n^{2}=\frac{1}{2}PN^{2}$.
如图②，延长PH交ND于点G，则PG⊥ND.
在Rt△PGN中，PN²=PG²+GN²=(m+n)²+(m−n)².
易得$AD=\frac{\sqrt{3}}{3}m$，$BF=\frac{\sqrt{3}}{3}n$.
∵AD+DE+EF+BF=AB，
∴$\frac{\sqrt{3}}{3}m+m+n+\frac{\sqrt{3}}{3}n=\sqrt{3}+3$，化简得m+n=3.
∴$S=\frac{1}{2}[3^{2}+(m−n)^{2}]=\frac{9}{2}+\frac{1}{2}(m−n)^{2}$.
①当(m−n)²=0，即m=n时，S最小，$S_{最小}=\frac{9}{2}$.
②当(m−n)²最大时，S最大，
即当m最大且n最小时，S最大.
由
(2)知，$m_{最大}=3\sqrt{3}−3$.
∵m+n=3，
∴$n_{最小}=3−(3\sqrt{3}−3)=6−3\sqrt{3}$.
∴$S_{最大}=\frac{1}{2}[9+(m_{最大}−n_{最小})^{2}]=\frac{1}{2}[9+(3\sqrt{3}−3−6+3\sqrt{3})^{2}]=99−54\sqrt{3}$.
综上所述，这两个正方形面积和的最大值是$99−54\sqrt{3}$，最小值是$\frac{9}{2}$.