第101页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 如图,在□ABCD中,点E在CD上,若DE:CE= 1:2,则△CEF与△ABF的周长比为(

A. 1:2
B. 1:3
C. 2:3
D. 4:9
C
)
A. 1:2
B. 1:3
C. 2:3
D. 4:9
答案:
C [点拨]
∵四边形ABCD是平行四边形,
∴DC//AB,CD=AB.
∴易得△CEF∽△ABF.
∵DE:CE=1:2,
∴EC:DC=EC:AB=2:3.
∴△CEF与△ABF的周长比为2:3. 故选C.
∵四边形ABCD是平行四边形,
∴DC//AB,CD=AB.
∴易得△CEF∽△ABF.
∵DE:CE=1:2,
∴EC:DC=EC:AB=2:3.
∴△CEF与△ABF的周长比为2:3. 故选C.
2. 如图,点O是五边形ABCDE和五边形$A_1B_1C_1D_1E_1$的位似中心,若$OA:OA_1= 1:3,$则$C_1D_1:CD$等于(

A. 1:2
B. 1:3
C. 3:1
D. 4:1
C
)
A. 1:2
B. 1:3
C. 3:1
D. 4:1
答案:
C [点拨]由题意可得五边形ABCDE与五边形A₁B₁C₁D₁E₁的相似比为1:3,
∴CD:C₁D₁=1:3,即C₁D₁:CD=3:1. 故选C.
∴CD:C₁D₁=1:3,即C₁D₁:CD=3:1. 故选C.
3. 如图,在△ABC中,D,E分别为线段BC,BA的中点,设△ABC的面积为S₁,△EBD的面积为S₂,则$\frac{S_{2}}{S_{1}}$= (

A. $\frac{1}{2}$
B. $\frac{1}{4}$
C. $\frac{3}{4}$
D. $\frac{7}{8}$
B
)
A. $\frac{1}{2}$
B. $\frac{1}{4}$
C. $\frac{3}{4}$
D. $\frac{7}{8}$
答案:
B [点拨]由已知条件可知$\frac{BE}{AB}=\frac{BD}{BC}=\frac{1}{2}$,又因为∠B=∠B,所以△EBD∽△ABC;所以$\frac{S_{\triangle EBD}}{S_{\triangle ABC}}=(\frac{1}{2})^{2}=\frac{1}{4}$,故选B.
4. [2024常州武进区期末]如图,在平面直角坐标系中,以原点O为位似中心,若A点的坐标为(1,2),C点的坐标为(2,4),AB= $\sqrt{5}$,则线段CD的长为(

A. 2
B. 4
C. 2$\sqrt{5}$
D. $\sqrt{5}$
C
)
A. 2
B. 4
C. 2$\sqrt{5}$
D. $\sqrt{5}$
答案:
C
5. 情境题 生活应用 如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.5m,踏板DE的长为1.8m,支撑点A到踏脚点D的距离为1m,原来捣头点E着地,现在踏脚点D着地,则捣头点E上升了( )

A. 1.5m
B. 1.2m
C. 1m
D. 0.9m

A. 1.5m
B. 1.2m
C. 1m
D. 0.9m
答案:
D [点拨]示意图如图所示.
由题意可得AB//EF,
∴∠DAB=∠DEF,∠ABD=∠EFD.
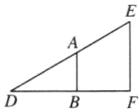
∴△DAB∽△DEF.
∴$\frac{AD}{DE}=\frac{AB}{EF}$,
∴$\frac{1}{1.8}=\frac{0.5}{EF}$.
∴EF=0.9米,即捣头点E上升了0.9米. 故选D.
D [点拨]示意图如图所示.
由题意可得AB//EF,
∴∠DAB=∠DEF,∠ABD=∠EFD.

∴△DAB∽△DEF.
∴$\frac{AD}{DE}=\frac{AB}{EF}$,
∴$\frac{1}{1.8}=\frac{0.5}{EF}$.
∴EF=0.9米,即捣头点E上升了0.9米. 故选D.
6. [2024衡水五中模拟]如图,点A,B都在格点上,若BC= $\frac{2\sqrt{13}}{3}$,则AC的长为(

A. $\sqrt{13}$
B. $\frac{4\sqrt{13}}{3}$
C. 2$\sqrt{13}$
D. 3$\sqrt{13}$
B
)
A. $\sqrt{13}$
B. $\frac{4\sqrt{13}}{3}$
C. 2$\sqrt{13}$
D. 3$\sqrt{13}$
答案:
B
7. 由12个有公共顶点O的直角三角形拼成如图所示的图形.∠AOB= ∠BOC= ∠COD=… =∠LOM= 30°.若S△AOB= 1,则图中与△AOB位似的三角形的面积为(

A. ($\frac{4}{3}$)^3
B. ($\frac{4}{3}$)^7
C. ($\frac{4}{3}$)^6
D. ($\frac{3}{4}$)^6
C
)
A. ($\frac{4}{3}$)^3
B. ($\frac{4}{3}$)^7
C. ($\frac{4}{3}$)^6
D. ($\frac{3}{4}$)^6
答案:
C [点拨]在Rt△AOB中,∠AOB=30°,
∴OB=$\frac{2}{\sqrt{3}}$OA.
同理OC=$\frac{2}{\sqrt{3}}$OB,
∴OC=$(\frac{2}{\sqrt{3}})^{2}$OA.
同理OD=$(\frac{2}{\sqrt{3}})^{3}$OA,……,OG=$(\frac{2}{\sqrt{3}})^{6}$OA.
由位似图形的概念可知,△GOH与△AOB位似,且相似比为OG:OA=$(\frac{2}{\sqrt{3}})^{6}$:1.
∵S△AOB=1,
∴S△GOH=$[(\frac{2}{\sqrt{3}})^{6}]^{2}=(\frac{4}{3})^{6}$. 故选C.
∴OB=$\frac{2}{\sqrt{3}}$OA.
同理OC=$\frac{2}{\sqrt{3}}$OB,
∴OC=$(\frac{2}{\sqrt{3}})^{2}$OA.
同理OD=$(\frac{2}{\sqrt{3}})^{3}$OA,……,OG=$(\frac{2}{\sqrt{3}})^{6}$OA.
由位似图形的概念可知,△GOH与△AOB位似,且相似比为OG:OA=$(\frac{2}{\sqrt{3}})^{6}$:1.
∵S△AOB=1,
∴S△GOH=$[(\frac{2}{\sqrt{3}})^{6}]^{2}=(\frac{4}{3})^{6}$. 故选C.
8. 如图所示的是一个由A,B,C三种相似的直角三角形纸片(C与B,B与A的相似比相同)拼成的矩形,相邻纸片之间互不重叠也无缝隙,其中A,B,C的纸片的面积分别$S_1,S_2,S_3,$若$S_1>S_2>S_3,$则这个矩形的面积一定可以表示为( )
$A. 4S_1$
$B. 6S_2$
$C. 4S_2+3S_3$
$D. 3S_1+4S_3$

$A. 4S_1$
$B. 6S_2$
$C. 4S_2+3S_3$
$D. 3S_1+4S_3$

答案:
A [点拨]如图,由A,B,C三种直角三角形相似,设C与B,B与A的相似比为k,EF=m,则GH=mk,FH=mk².

∴EH=m(1+k²),
FM=$\frac{m(1+k²)}{k}$,
FK=km(1+k²).
由题意得km(1+k²)+mk=$\frac{m(1+k²)}{k}$,
整理得k⁴+k²−1=0,
∴k²=$\frac{-1+\sqrt{5}}{2}$或$\frac{-1-\sqrt{5}}{2}$(舍去).
∴S₂=$\frac{-1+\sqrt{5}}{2}$S₁,S₃=$(\frac{-1+\sqrt{5}}{2})^{2}$S₁=$\frac{3-\sqrt{5}}{2}$S₁.
∴S₂+S₃=S₁.
∴这个矩形的面积=2S₁+2(S₂+S₃)=4S₁,
故选A.
A [点拨]如图,由A,B,C三种直角三角形相似,设C与B,B与A的相似比为k,EF=m,则GH=mk,FH=mk².

∴EH=m(1+k²),
FM=$\frac{m(1+k²)}{k}$,
FK=km(1+k²).
由题意得km(1+k²)+mk=$\frac{m(1+k²)}{k}$,
整理得k⁴+k²−1=0,
∴k²=$\frac{-1+\sqrt{5}}{2}$或$\frac{-1-\sqrt{5}}{2}$(舍去).
∴S₂=$\frac{-1+\sqrt{5}}{2}$S₁,S₃=$(\frac{-1+\sqrt{5}}{2})^{2}$S₁=$\frac{3-\sqrt{5}}{2}$S₁.
∴S₂+S₃=S₁.
∴这个矩形的面积=2S₁+2(S₂+S₃)=4S₁,
故选A.
9. [2023鄂州]如图,在平面直角坐标系中,△ABC与△A₁B₁C₁位似,原点O是位似中心,且$\frac{AB}{A_{1}B_{1}}$= 3.若A(9,3),则A₁的坐标是

(3,1)
.
答案:
(3,1)
10. 如果两个相似三角形的最长边分别是35cm和14cm,它们的周长之差为60cm,那么这两个三角形的周长分别是
100cm和40cm
.
答案:
100cm和40cm [点拨]
∵两个相似三角形的相似比为$\frac{35}{14}=\frac{5}{2}$,
∴它们的周长比为$\frac{5}{2}$.
∴可设较大三角形的周长为5xcm,则较小三角形的周长为2xcm.
∵它们的周长之差为60cm,
∴5x−2x=60,解得x=20.
∴这两个三角形的周长分别为100cm和40cm.
∵两个相似三角形的相似比为$\frac{35}{14}=\frac{5}{2}$,
∴它们的周长比为$\frac{5}{2}$.
∴可设较大三角形的周长为5xcm,则较小三角形的周长为2xcm.
∵它们的周长之差为60cm,
∴5x−2x=60,解得x=20.
∴这两个三角形的周长分别为100cm和40cm.
查看更多完整答案,请扫码查看


