第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 情境题·敬老爱老 “敬老爱老”是中华民族的优秀传统美德. 小刚、小强计划利用暑假从A,B,C三处养老服务中心中随机选择一处参加志愿服务活动,则两人恰好选到同一处的概率是(
A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{6}$
D. $\frac{2}{9}$
B
)A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{6}$
D. $\frac{2}{9}$
答案:
B
2. 新趋势·学科内综合 设圆锥的半径为r,高为h. 下面有几个圆锥:①$r= \sqrt{2},h= \frac{1}{2}$;②$r= \frac{1}{3},h= 3$;③$r= \frac{1}{2},h= 4$;④$r= 1,h= 1$;从上面圆锥中任取两个,则两者体积相同的概率是(
A. $\frac{1}{3}$
B. $\frac{1}{6}$
C. $\frac{2}{3}$
D. $\frac{1}{2}$
D
)A. $\frac{1}{3}$
B. $\frac{1}{6}$
C. $\frac{2}{3}$
D. $\frac{1}{2}$
答案:
D
3. 用如图所示的两个可以自由转动的转盘做“配紫色”游戏,分别旋转两个转盘,若其中一个转盘转出红色,另一个转盘转出蓝色即可配成紫色,则可配成紫色的概率是(
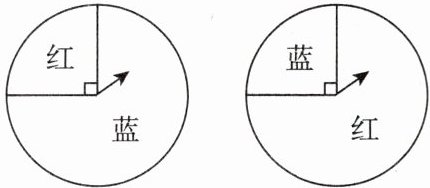
A. $\frac{3}{8}$
B. $\frac{1}{2}$
C. $\frac{5}{8}$
D. $\frac{2}{3}$
C
)
A. $\frac{3}{8}$
B. $\frac{1}{2}$
C. $\frac{5}{8}$
D. $\frac{2}{3}$
答案:
C
4. [2024武汉模拟] 看了《田忌赛马》的故事后,小杨用数学模型来分析:齐王与田忌的上、中、下三个等级的三匹马综合指标数如表所示,每匹马只赛一场,综合指标的两数相比,大数为胜,三场两胜则赢,已知齐王的三匹马出场顺序为6,4,2. 若田忌的三匹马随机出场,则田忌能赢得比赛的概率为(
|马匹等级|下等马|中等马|上等马|
|----|----|----|----|
|齐王|2|4|6|
|田忌|1|3|5|
A. $\frac{1}{3}$
B. $\frac{1}{6}$
C. $\frac{1}{9}$
D. $\frac{1}{12}$
B
)|马匹等级|下等马|中等马|上等马|
|----|----|----|----|
|齐王|2|4|6|
|田忌|1|3|5|
A. $\frac{1}{3}$
B. $\frac{1}{6}$
C. $\frac{1}{9}$
D. $\frac{1}{12}$
答案:
B 【点拨】由于田忌的上、中等马分别比齐王的中、下等马强,当齐王的三匹马出场顺序为6,4,2时,田忌的马按1,5,3的顺序出场,田忌才能赢得比赛,当田忌的三匹马随机出场时,双方马的对阵情况如下:
|齐王的马|上中下|上中下|上中下|上中下|上中下|上中下|
|----|----|----|----|----|----|----|
|田忌的马|上中下|上下中|中上下|中下上|下中上|下中上|
双方马的对阵中,只有一种对阵情况田忌能赢,
∴田忌能赢得比赛的概率为$\frac {1}{6}$.
故选 B.
|齐王的马|上中下|上中下|上中下|上中下|上中下|上中下|
|----|----|----|----|----|----|----|
|田忌的马|上中下|上下中|中上下|中下上|下中上|下中上|
双方马的对阵中,只有一种对阵情况田忌能赢,
∴田忌能赢得比赛的概率为$\frac {1}{6}$.
故选 B.
5. 有两组卡片,卡片除正面写有不同字母外其他都相同. 第一组卡片上写有a,b,b,第二组卡片上写有a,b,b,c,现将两组卡片背面朝上分别洗匀,求从每组卡片中各随机抽取一张,都抽到b的概率是(
A. $\frac{5}{12}$
B. $\frac{1}{3}$
C. $\frac{1}{4}$
D. $\frac{4}{9}$
B
)A. $\frac{5}{12}$
B. $\frac{1}{3}$
C. $\frac{1}{4}$
D. $\frac{4}{9}$
答案:
B 【点拨】
由表可知,共有12种等可能的结果,其中从每组卡片中各随机抽取一张,都抽到b的结果有4种,
∴从每组卡片中各随机抽取一张,都抽到b的概率为$\frac {4}{12}=\frac {1}{3}$.
由表可知,共有12种等可能的结果,其中从每组卡片中各随机抽取一张,都抽到b的结果有4种,
∴从每组卡片中各随机抽取一张,都抽到b的概率为$\frac {4}{12}=\frac {1}{3}$.
6. 新趋势·跨学科 如图所示,电路连接完好,且各元件工作正常. 随机闭合开关$S_{1},S_{2},S_{3},S_{4}$中的两个,能让小灯泡发光的概率是( )
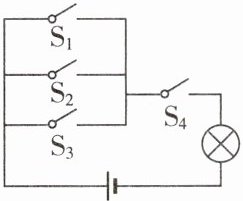
A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{4}$
D. $\frac{3}{4}$

A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{4}$
D. $\frac{3}{4}$
答案:
A 【点拨】画树状图如图:

由树状图可知,共有12种等可能的结果,其中能让小灯泡发光的结果有6种,
∴能让小灯泡发光的概率为$\frac {6}{12}=\frac {1}{2}$.
A 【点拨】画树状图如图:

由树状图可知,共有12种等可能的结果,其中能让小灯泡发光的结果有6种,
∴能让小灯泡发光的概率为$\frac {6}{12}=\frac {1}{2}$.
7. 有三张正面分别写着2,3,4,其他看上去无差别的卡片,从中随机抽取一张后,放回并混合在一起,再随机抽取一张,两次取出的数字之和是奇数的概率为
$\frac {4}{9}$
.
答案:
$\frac {4}{9}$
8. [2023广州] 甲、乙两名同学相约打乒乓球.
(1)有款式完全相同的4个乒乓球拍(分别记为A,B,C,D),若甲先从中随机选取1个,乙再从余下的球拍中随机选取1个,求乙选中球拍C的概率;
(2)双方约定:两人各投掷一枚质地均匀的硬币,如果两枚硬币全部正面朝上或全部反面朝上,那么甲先发球,否则乙先发球. 这个约定是否公平? 为什么?
(1)有款式完全相同的4个乒乓球拍(分别记为A,B,C,D),若甲先从中随机选取1个,乙再从余下的球拍中随机选取1个,求乙选中球拍C的概率;
(2)双方约定:两人各投掷一枚质地均匀的硬币,如果两枚硬币全部正面朝上或全部反面朝上,那么甲先发球,否则乙先发球. 这个约定是否公平? 为什么?
答案:
【解】(1)画树状图如图:

由树状图可知,共有12种等可能的结果,其中乙选中球拍C的结果有3种,
∴$P$(乙选中球拍$C)=\frac {3}{12}=\frac {1}{4}$.
(2)这个约定公平.理由如下:
画树状图如图:

由树状图可知,共有4种等可能的结果,其中两枚硬币全部正面朝上或全部反面朝上的结果有2种,
∴$P$(甲先发球)$=\frac {2}{4}=\frac {1}{2}$.
∴$P$(乙先发球)$=1-\frac {1}{2}=\frac {1}{2}$.
∵$P$(甲先发球)$=P$(乙先发球),
∴这个约定公平.
【解】(1)画树状图如图:

由树状图可知,共有12种等可能的结果,其中乙选中球拍C的结果有3种,
∴$P$(乙选中球拍$C)=\frac {3}{12}=\frac {1}{4}$.
(2)这个约定公平.理由如下:
画树状图如图:

由树状图可知,共有4种等可能的结果,其中两枚硬币全部正面朝上或全部反面朝上的结果有2种,
∴$P$(甲先发球)$=\frac {2}{4}=\frac {1}{2}$.
∴$P$(乙先发球)$=1-\frac {1}{2}=\frac {1}{2}$.
∵$P$(甲先发球)$=P$(乙先发球),
∴这个约定公平.
查看更多完整答案,请扫码查看


