第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 下列方程中,一定是一元二次方程的是(
A. $\frac {1}{y^{2}}+y= 2$
B. $x(x-1)= x^{2}-3x-2$
C. $ax^{2}+bx+c= 0$
D. $2x^{2}-x= 0$
D
)A. $\frac {1}{y^{2}}+y= 2$
B. $x(x-1)= x^{2}-3x-2$
C. $ax^{2}+bx+c= 0$
D. $2x^{2}-x= 0$
答案:
D【点拨】A. 方程中含有分式,不是一元二次方程;
B. 方程化简后是一元一次方程,不是一元二次方程;C. 当
$ a = 0 $时,方程不是一元二次方程;D. 符合一元二次方程的
特征,是一元二次方程. 故选 D.
B. 方程化简后是一元一次方程,不是一元二次方程;C. 当
$ a = 0 $时,方程不是一元二次方程;D. 符合一元二次方程的
特征,是一元二次方程. 故选 D.
2. [2023西安交大附中期中]一元二次方程$x^{2}-8x-2= 0$,配方后可变形为(
A. $(x-4)^{2}= 18$
B. $(x-4)^{2}= 14$
C. $(x-8)^{2}= 64$
D. $(x-4)^{2}= 1$
A
)A. $(x-4)^{2}= 18$
B. $(x-4)^{2}= 14$
C. $(x-8)^{2}= 64$
D. $(x-4)^{2}= 1$
答案:
A【点拨】方程移项得$ x^{2}-8x=2 $,配方得$ x^{2}-8x + $
$ 16=2 + 16 $,即$ (x - 4)^{2}=18 $。故选 A.
$ 16=2 + 16 $,即$ (x - 4)^{2}=18 $。故选 A.
3. 解方程$x-\sqrt {2}= (\sqrt {2}-x)^{2}$,最合适的方法是(
A. 配方法
B. 因式分解法
C. 公式法
D. 直接开平方法
B
)A. 配方法
B. 因式分解法
C. 公式法
D. 直接开平方法
答案:
B
4. 母题 教材P43习题T1 一元二次方程$2x^{2}+x-1= 0$的根的情况是(
A. 有两个不相等的实数根
B. 有两个相等的实数根
C. 只有一个实数根
D. 没有实数根
A
)A. 有两个不相等的实数根
B. 有两个相等的实数根
C. 只有一个实数根
D. 没有实数根
答案:
A【点拨】$ \because \Delta =1^{2}-4×2×(-1)=9>0 $,$ \therefore $方程有两
个不相等的实数根,故选 A.
个不相等的实数根,故选 A.
5. [2024深圳模拟]“立身以立学为先,立学以读书为本.”为了鼓励全民阅读,某校图书馆开展阅读活动,自阅读活动开展以来,进馆阅读人次逐月增加,第一个月进馆200人次,前三个月累计进馆728人次,若进馆人次的月增长率相同,求进馆人次的月增长率,设进馆人次的月增长率为$x$,依题意可列方程为(
A. $200(1+x)^{2}= 728$
B. $200(1+x)+200(1+x)^{2}= 728$
C. $200(1+x+x^{2})= 728$
D. $200+200(1+x)+200(1+x)^{2}= 728$
D
)A. $200(1+x)^{2}= 728$
B. $200(1+x)+200(1+x)^{2}= 728$
C. $200(1+x+x^{2})= 728$
D. $200+200(1+x)+200(1+x)^{2}= 728$
答案:
D
6. 情境题 地域文化 “房子半边盖”是陕西十大怪之一,这种房子的结构是“人”字结构房屋的一半.如图所示的是这种房子的屋架,$∠ACB= 90^{\circ }$,$D是AB$的中点,$AC= a\ m$,$BC= b\ m$,若$a$,$b恰好是方程x^{2}-x= 4(x-1)$的两个实数根,则$CD$的长是(
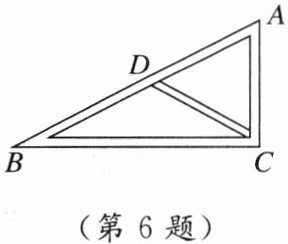
A. $1\ m$
B. $4\ m$
C. $\sqrt {17}\ m$
D. $\frac {\sqrt {17}}{2}\ m$
D
)
A. $1\ m$
B. $4\ m$
C. $\sqrt {17}\ m$
D. $\frac {\sqrt {17}}{2}\ m$
答案:
D
7. 若关于$x的方程x^{2}+2x-3= 0与\frac {2}{x+3}= \frac {1}{x-a}$有一个解相同,则$a$的值为(
A. $1$
B. $1或-3$
C. $-1$
D. $-1或3$
C
)A. $1$
B. $1或-3$
C. $-1$
D. $-1或3$
答案:
C【点拨】解方程$ x^{2}+2x - 3=0 $,得$ x_{1}=1,x_{2}=-3 $。由
分式方程可知$ x=-3 $不是分式方程的解. 把$ x = 1 $代入分
式方程,得$ \frac{2}{1 + 3}=\frac{1}{1 - a} $,解得$ a=-1 $。经检验,$ a=-1 $是分
式方程$ \frac{2}{1 + 3}=\frac{1}{1 - a} $的解,$ \therefore a=-1 $,故选 C.
分式方程可知$ x=-3 $不是分式方程的解. 把$ x = 1 $代入分
式方程,得$ \frac{2}{1 + 3}=\frac{1}{1 - a} $,解得$ a=-1 $。经检验,$ a=-1 $是分
式方程$ \frac{2}{1 + 3}=\frac{1}{1 - a} $的解,$ \therefore a=-1 $,故选 C.
8. 欧几里得的《几何原本》中记载了形如$x^{2}-2bx+4c^{2}= 0(b>2c>0)$的方程根的图形解法:如图,画$Rt\triangle ABC$,使$∠ACB= 90^{\circ }$,$AC= 2c$,$AB= b$,以点$B$为圆心,$BC$为半径画圆,交射线$AB于点D$,$E$,则该方程较大的根是(
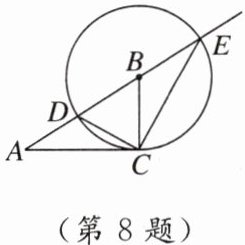
A. $CE$的长度
B. $AE$的长度
C. $DE$的长度
D. $CD$的长度
B
)
A. $CE$的长度
B. $AE$的长度
C. $DE$的长度
D. $CD$的长度
答案:
B【点拨】$ \because x^{2}-2bx + 4c^{2}=0 $,
$ \therefore x^{2}-2bx=-4c^{2} $,则$ x^{2}-2bx + b^{2}=b^{2}-4c^{2} $,
$ \therefore (x - b)^{2}=b^{2}-4c^{2} $,
$ \therefore x - b=\pm \sqrt{b^{2}-4c^{2}} $,
$ \therefore x_{1}=b + \sqrt{b^{2}-4c^{2}},x_{2}=b - \sqrt{b^{2}-4c^{2}} $,
在$ Rt\triangle ABC $中,$ \angle ACB = 90^{\circ},AC = 2c,AB = b $,
$ \therefore BC=\sqrt{AB^{2}-BC^{2}}=\sqrt{b^{2}-4c^{2}} $,
$ \therefore $方程较大的根为$ AB + BC = AB + BE = AE $的长度,
故选 B.
$ \therefore x^{2}-2bx=-4c^{2} $,则$ x^{2}-2bx + b^{2}=b^{2}-4c^{2} $,
$ \therefore (x - b)^{2}=b^{2}-4c^{2} $,
$ \therefore x - b=\pm \sqrt{b^{2}-4c^{2}} $,
$ \therefore x_{1}=b + \sqrt{b^{2}-4c^{2}},x_{2}=b - \sqrt{b^{2}-4c^{2}} $,
在$ Rt\triangle ABC $中,$ \angle ACB = 90^{\circ},AC = 2c,AB = b $,
$ \therefore BC=\sqrt{AB^{2}-BC^{2}}=\sqrt{b^{2}-4c^{2}} $,
$ \therefore $方程较大的根为$ AB + BC = AB + BE = AE $的长度,
故选 B.
9. [2024天津一中月考]已知关于$x的方程(m-1)\cdot x^{m^{2}+1}+2x-3= 0$是一元二次方程,则$m$的值为
-1
.
答案:
-1
10. 若关于$x的方程x^{2}+x+c= 0$有两个相等的实数根,则实数$c$的值为
$\frac{1}{4}$
.
答案:
$ \frac{1}{4} $【点拨】由题意得$ 1 - 4c = 0 $,则$ c=\frac{1}{4} $。
11. 新考法 整体代入法 已知$m是一元二次方程x^{2}+x-6= 0$的一个根,则代数式$m^{3}+2m^{2}-5m+6$的值等于______
12
.
答案:
12【点拨】$ \because m $是一元二次方程$ x^{2}+x - 6=0 $的一个
根,$ \therefore m^{2}+m - 6=0 $,即$ m^{2}+m = 6 $。
$ \therefore m^{3}+2m^{2}-5m + 6=m^{3}+m^{2}+m^{2}-5m + 6=m(m^{2}+ $
$ m)+m^{2}-5m + 6=6m + m^{2}-5m + 6=m^{2}+m + 6=6 + $
$ 6=12 $。
根,$ \therefore m^{2}+m - 6=0 $,即$ m^{2}+m = 6 $。
$ \therefore m^{3}+2m^{2}-5m + 6=m^{3}+m^{2}+m^{2}-5m + 6=m(m^{2}+ $
$ m)+m^{2}-5m + 6=6m + m^{2}-5m + 6=m^{2}+m + 6=6 + $
$ 6=12 $。
12. 新考法 数形结合法 一个直角三角形的两条直角边之差是$2\ cm$,面积是$24\ cm^{2}$,则较长的直角边的长是______
8 cm
.
答案:
8 cm【点拨】设较长的直角边的长为$ x $cm. 由题意可得
$ \frac{1}{2}x(x - 2)=24 $,解得$ x_{1}=8,x_{2}=-6 $(舍去). 故较长的直角
边的长是8 cm.
$ \frac{1}{2}x(x - 2)=24 $,解得$ x_{1}=8,x_{2}=-6 $(舍去). 故较长的直角
边的长是8 cm.
查看更多完整答案,请扫码查看


