第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. [2023朔州期末] 两个矩形的位置如图所示,若$∠1= 115^{\circ }$,则$∠2= $ (
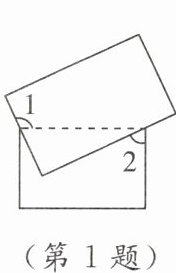
A.$50^{\circ }$
B.$55^{\circ }$
C.$60^{\circ }$
D.$65^{\circ }$
D
)
A.$50^{\circ }$
B.$55^{\circ }$
C.$60^{\circ }$
D.$65^{\circ }$
答案:
D
2. 2023·株洲 一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图所示,已知$∠ACB= 90^{\circ }$,点D为边AB的中点,点A,B对应的刻度为1,7,则$CD= $ (
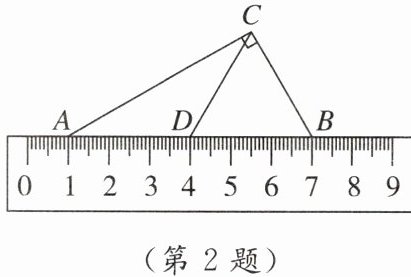
A. 3.5 cm
B. 3 cm
C. 4.5 cm
D. 6 cm
B
)
A. 3.5 cm
B. 3 cm
C. 4.5 cm
D. 6 cm
答案:
B
3. [2023上海黄浦区期中] 如图,在矩形ABCD中,$AB= 1,AD= 2$,点M在边BC上,若MA平分$∠DMB$,则CM的长是 (
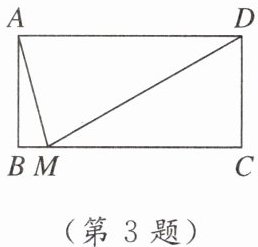
A.$3\sqrt {2}$
B. 1
C.$2\sqrt {5}$
D.$\sqrt {3}$
D
)
A.$3\sqrt {2}$
B. 1
C.$2\sqrt {5}$
D.$\sqrt {3}$
答案:
D
4. 2023·舟山模拟 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,根据图形可知他得出的这个推论指 (

A.$S_{矩形ABMN}= S_{矩形MNDC}$
B.$S_{矩形EBMF}= S_{矩形AEFN}$
C.$S_{矩形AEFN}= S_{矩形MNDC}$
D.$S_{矩形EBMF}= S_{矩形NFGD}$
D
)
A.$S_{矩形ABMN}= S_{矩形MNDC}$
B.$S_{矩形EBMF}= S_{矩形AEFN}$
C.$S_{矩形AEFN}= S_{矩形MNDC}$
D.$S_{矩形EBMF}= S_{矩形NFGD}$
答案:
D
5. 情境题 振兴乡村旅游业 明明的家乡有一片矩形“油菜花田”,政府决定在矩形油菜花田上建两条如图所示的小路AC,BD,方便游客(不考虑路宽),已知$AB= 30m$,BC= 40m,那么两条小路的总长为
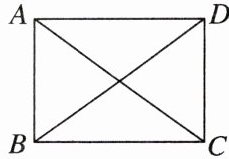
100 m
.
答案:
100 m
6. 如图,在矩形ABCD中,点E在BC上,$AE= AD,DF⊥AE$,垂足为F.
(1)求证:$DF= AB$.
证明:在矩形 $ABCD$ 中,$AD // BC$,$\angle B = 90^{\circ}$,
$\therefore \angle AEB = \angle DAF$。
$\because DF \perp AE$,$\therefore \angle DFA = 90^{\circ} = \angle B$。
在 $\triangle ADF$ 和 $\triangle EAB$ 中,$\left\{\begin{array}{l} \angle DFA = \angle B, \\ \angle DAF = \angle AEB, \\ AD = EA, \end{array}\right.$
$\therefore \triangle ADF \cong \triangle EAB$(
$\therefore DF = AB$。
(2)若$∠FDC= 30^{\circ }$,且$AB= 4$,求AD的长.
解:$\because \angle ADF + \angle FDC = 90^{\circ}$,$\angle DAF + \angle ADF = 90^{\circ}$,
$\therefore \angle DAF = \angle FDC = 30^{\circ}$。
$\therefore AD = 2DF$。
又 $\because DF = AB$,$\therefore AD = 2AB =$
(1)求证:$DF= AB$.
证明:在矩形 $ABCD$ 中,$AD // BC$,$\angle B = 90^{\circ}$,
$\therefore \angle AEB = \angle DAF$。
$\because DF \perp AE$,$\therefore \angle DFA = 90^{\circ} = \angle B$。
在 $\triangle ADF$ 和 $\triangle EAB$ 中,$\left\{\begin{array}{l} \angle DFA = \angle B, \\ \angle DAF = \angle AEB, \\ AD = EA, \end{array}\right.$
$\therefore \triangle ADF \cong \triangle EAB$(
AAS
)。$\therefore DF = AB$。
(2)若$∠FDC= 30^{\circ }$,且$AB= 4$,求AD的长.
解:$\because \angle ADF + \angle FDC = 90^{\circ}$,$\angle DAF + \angle ADF = 90^{\circ}$,
$\therefore \angle DAF = \angle FDC = 30^{\circ}$。
$\therefore AD = 2DF$。
又 $\because DF = AB$,$\therefore AD = 2AB =$
8
。
答案:
(1)【证明】在矩形 $ABCD$ 中,$AD // BC$,$\angle B = 90^{\circ}$,
$\therefore \angle AEB = \angle DAF$。
$\because DF \perp AE$,$\therefore \angle DFA = 90^{\circ} = \angle B$。
在 $\triangle ADF$ 和 $\triangle EAB$ 中,$\left\{\begin{array}{l} \angle DFA = \angle B, \\ \angle DAF = \angle AEB, \\ AD = EA, \end{array}\right.$
$\therefore \triangle ADF \cong \triangle EAB(AAS)$。
$\therefore DF = AB$。
(2)【解】$\because \angle ADF + \angle FDC = 90^{\circ}$,$\angle DAF + \angle ADF = 90^{\circ}$,
$\therefore \angle DAF = \angle FDC = 30^{\circ}$。
$\therefore AD = 2DF$。
又 $\because DF = AB$,$\therefore AD = 2AB = 8$。
(1)【证明】在矩形 $ABCD$ 中,$AD // BC$,$\angle B = 90^{\circ}$,
$\therefore \angle AEB = \angle DAF$。
$\because DF \perp AE$,$\therefore \angle DFA = 90^{\circ} = \angle B$。
在 $\triangle ADF$ 和 $\triangle EAB$ 中,$\left\{\begin{array}{l} \angle DFA = \angle B, \\ \angle DAF = \angle AEB, \\ AD = EA, \end{array}\right.$
$\therefore \triangle ADF \cong \triangle EAB(AAS)$。
$\therefore DF = AB$。
(2)【解】$\because \angle ADF + \angle FDC = 90^{\circ}$,$\angle DAF + \angle ADF = 90^{\circ}$,
$\therefore \angle DAF = \angle FDC = 30^{\circ}$。
$\therefore AD = 2DF$。
又 $\because DF = AB$,$\therefore AD = 2AB = 8$。
7. 易错题 如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离 (
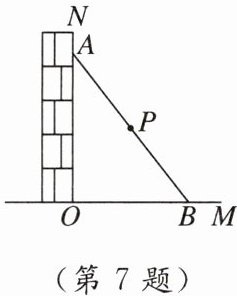
A. 变小
B. 不变
C. 变大
D. 无法判断
B
)
A. 变小
B. 不变
C. 变大
D. 无法判断
答案:
B
8. 新考法 折叠法 如图,折叠矩形纸片ABCD,使点B的对应点E落在CD边上,GH为折痕,已知$AB= 6,BC= 10$.当折痕GH最长时,线段BH的长为
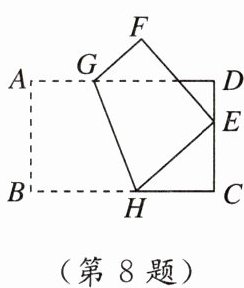
6.8
.
答案:
6.8 【点拨】在 $E$ 点从 $C$ 点移动到 $D$ 点的过程中,$\angle CHE$ 变大而 $\angle GHB$ 变小,纸片宽度不变,故当 $E$ 点与 $D$ 点重合时,$GH$ 最长。
设 $BH = x$,则 $CH = 10 - x$,$HE = BH = x$。
由勾股定理得,$HC^{2} + CE^{2} = HE^{2}$,
即 $(10 - x)^{2} + 6^{2} = x^{2}$,解得 $x = 6.8$。
设 $BH = x$,则 $CH = 10 - x$,$HE = BH = x$。
由勾股定理得,$HC^{2} + CE^{2} = HE^{2}$,
即 $(10 - x)^{2} + 6^{2} = x^{2}$,解得 $x = 6.8$。
查看更多完整答案,请扫码查看


