第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. [2024保定模拟] 下列图形一定为矩形的是(
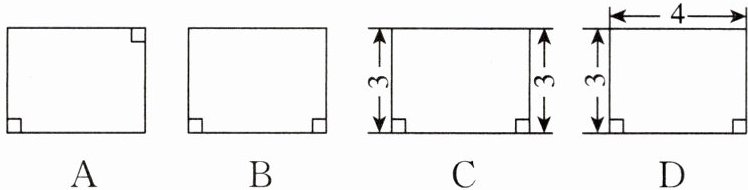
C
)
答案:
C
2. 情境题 生活应用 李师傅要做一个矩形桌面,做好后量得一对长边长为80 cm,一对短边长为60 cm,对角线长为100 cm,则这个桌面
合格
(填“合格”或“不合格”).
答案:
合格
3. [2023廊坊期末] 在平面直角坐标系中,已知点A(-2,-1),点B(2,3),点C(2,-1),在平面直角坐标系中找一点D,使以点A,B,C,D为顶点的四边形为矩形,则BD的长为
4
,点D的坐标为(-2,3)
.
答案:
4;$(-2,3)$
4. 易错题 如图,A,B为5×5的正方形网格中的两个格点,称四个顶点都是格点的矩形为格点矩形,在此图中以A,B为顶点的格点矩形共可以画出
4
个.
答案:
4
5. [2024恩施州模拟] 如图,在平行四边形ABCD中,对角线BD,AC相交于点O,AE⊥BD,BF⊥AC,垂足分别为E,F.若CF= DE,求证:四边形ABCD为矩形.
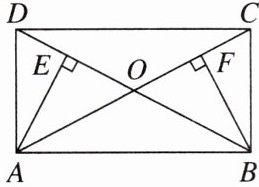
[证明]∵四边形ABCD是平行四边形,
∴$AD = BC$,$AD// BC$,$DO = \frac{1}{2}BD$,$AO = \frac{1}{2}AC$。
∴∠BCF = ∠DAO。
在Rt△ADE与Rt△BCF中,$\begin{cases}AD = BC\\DE = CF\end{cases}$
∴Rt△ADE≌Rt△BCF(
∴∠ADE = ∠BCF。
∴∠ADE = ∠DAO。
∴$DO = AO$。
∴$AC = BD$。
又∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形。

[证明]∵四边形ABCD是平行四边形,
∴$AD = BC$,$AD// BC$,$DO = \frac{1}{2}BD$,$AO = \frac{1}{2}AC$。
∴∠BCF = ∠DAO。
在Rt△ADE与Rt△BCF中,$\begin{cases}AD = BC\\DE = CF\end{cases}$
∴Rt△ADE≌Rt△BCF(
HL
)。∴∠ADE = ∠BCF。
∴∠ADE = ∠DAO。
∴$DO = AO$。
∴$AC = BD$。
又∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形。
答案:
[证明]
∵四边形ABCD是平行四边形,
∴$AD = BC$,$AD// BC$,$DO = \frac{1}{2}BD$,$AO = \frac{1}{2}AC$。
∴$∠BCF = ∠DAO$。
在$Rt△ADE$与$Rt△BCF$中,$\begin{cases}AD = BC\\DE = CF\end{cases}$
∴$Rt△ADE≌Rt△BCF(HL)$。
∴$∠ADE = ∠BCF$。
∴$∠ADE = ∠DAO$。
∴$DO = AO$。
∴$AC = BD$。
又
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形。
∵四边形ABCD是平行四边形,
∴$AD = BC$,$AD// BC$,$DO = \frac{1}{2}BD$,$AO = \frac{1}{2}AC$。
∴$∠BCF = ∠DAO$。
在$Rt△ADE$与$Rt△BCF$中,$\begin{cases}AD = BC\\DE = CF\end{cases}$
∴$Rt△ADE≌Rt△BCF(HL)$。
∴$∠ADE = ∠BCF$。
∴$∠ADE = ∠DAO$。
∴$DO = AO$。
∴$AC = BD$。
又
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形。
6. 如图,四边形ABCD是菱形,E,F,G,H分别是边AB,BC,CD,DA的中点,连接EF,FG,GH,HE.求证:四边形EFGH是矩形.
[证明]连接AC,BD,
∵E,F分别为AB,BC的中点,
∴EF为
∴
同理可得,
∴
∴四边形EFGH为
∵四边形ABCD是菱形,∴
∵
∵
∴
∴四边形EFGH是矩形。
[证明]连接AC,BD,
∵E,F分别为AB,BC的中点,
∴EF为
△ABC
的中位线。∴
EF// AC
且$EF = \frac{1}{2}AC$
。同理可得,
HG// AC
且$HG = \frac{1}{2}AC$
,EH// BD
。∴
EF// HG
且EF = HG
。∴四边形EFGH为
平行四边形
。∵四边形ABCD是菱形,∴
AC⊥BD
。∵
EF// AC
,∴EF⊥BD
。∵
EH// BD
,∴EH⊥EF
。∴
$∠FEH = 90^{\circ}$
。∴四边形EFGH是矩形。
答案:
[证明]连接AC,BD,
∵E,F分别为AB,BC的中点,
∴EF为$△ABC$的中位线。
∴$EF// AC$且$EF = \frac{1}{2}AC$。
同理可得,$HG// AC$且$HG = \frac{1}{2}AC$,$EH// BD$。
∴$EF// HG$且$EF = HG$。
∴四边形EFGH为平行四边形。
∵四边形ABCD是菱形,
∴$AC⊥BD$。
∵$EF// AC$,
∴$EF⊥BD$。
∵$EH// BD$,
∴$EH⊥EF$。
∴$∠FEH = 90^{\circ}$。
∴四边形EFGH是矩形。
∵E,F分别为AB,BC的中点,
∴EF为$△ABC$的中位线。
∴$EF// AC$且$EF = \frac{1}{2}AC$。
同理可得,$HG// AC$且$HG = \frac{1}{2}AC$,$EH// BD$。
∴$EF// HG$且$EF = HG$。
∴四边形EFGH为平行四边形。
∵四边形ABCD是菱形,
∴$AC⊥BD$。
∵$EF// AC$,
∴$EF⊥BD$。
∵$EH// BD$,
∴$EH⊥EF$。
∴$∠FEH = 90^{\circ}$。
∴四边形EFGH是矩形。
7. 新视角·动点探究题 如图,在四边形ABCD中,∠A= ∠B= 90°,AD= 10 cm,BC= 8 cm,点P从点D出发,以1 cm/s的速度向点A运动,同时点M从点B出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t s,下列结论正确的是( )
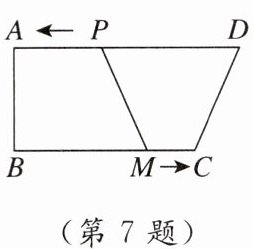
A. 当t= 4时,四边形ABMP为矩形
B. 当t= 5时,四边形CDPM为平行四边形
C. 当CD= PM时,t= 4
D. 当CD= PM时,t= 4或6

A. 当t= 4时,四边形ABMP为矩形
B. 当t= 5时,四边形CDPM为平行四边形
C. 当CD= PM时,t= 4
D. 当CD= PM时,t= 4或6
答案:
D [点拨]根据题意,可得$DP = tcm$,$BM = tcm$。
∵$AD = 10cm$,$BC = 8cm$,
∴$AP = (10 - t)cm$,$CM = (8 - t)cm$。
当四边形ABMP为矩形时,$AP = BM$,
即$10 - t = t$,解得$t = 5$,故A不正确;
当四边形CDPM为平行四边形时,$DP = CM$,
即$8 - t = t$,解得$t = 4$,故B不正确;
当$CD = PM$时,分两种情况:
当四边形CDPM是平行四边形时,$DP = CM$,
即$8 - t = t$,解得$t = 4$。
当四边形CDPM是等腰梯形时,
过点M作$MG⊥AD$于点G,过点C作$CH⊥AD$于点H,如图所示。
则$∠MGP = ∠CHD = 90^{\circ}$。
易知$GM = HC$。
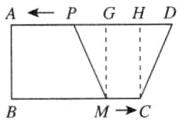
又
∵$CD = PM$,
∴$Rt△MGP≌Rt△CHD(HL)$。
∴$GP = HD = \frac{t - (8 - t)}{2}(cm)$。
∴$AG = AP + GP = [10 - t + \frac{t - (8 - t)}{2}]cm$。
又易知$BM = AG$,
∴$t = 10 - t + \frac{t - (8 - t)}{2}$,
解得$t = 6$。
综上可得,当$CD = PM$时,$t = 6$或$t = 4$,故C错误,D正确。
D [点拨]根据题意,可得$DP = tcm$,$BM = tcm$。
∵$AD = 10cm$,$BC = 8cm$,
∴$AP = (10 - t)cm$,$CM = (8 - t)cm$。
当四边形ABMP为矩形时,$AP = BM$,
即$10 - t = t$,解得$t = 5$,故A不正确;
当四边形CDPM为平行四边形时,$DP = CM$,
即$8 - t = t$,解得$t = 4$,故B不正确;
当$CD = PM$时,分两种情况:
当四边形CDPM是平行四边形时,$DP = CM$,
即$8 - t = t$,解得$t = 4$。
当四边形CDPM是等腰梯形时,
过点M作$MG⊥AD$于点G,过点C作$CH⊥AD$于点H,如图所示。
则$∠MGP = ∠CHD = 90^{\circ}$。
易知$GM = HC$。

又
∵$CD = PM$,
∴$Rt△MGP≌Rt△CHD(HL)$。
∴$GP = HD = \frac{t - (8 - t)}{2}(cm)$。
∴$AG = AP + GP = [10 - t + \frac{t - (8 - t)}{2}]cm$。
又易知$BM = AG$,
∴$t = 10 - t + \frac{t - (8 - t)}{2}$,
解得$t = 6$。
综上可得,当$CD = PM$时,$t = 6$或$t = 4$,故C错误,D正确。
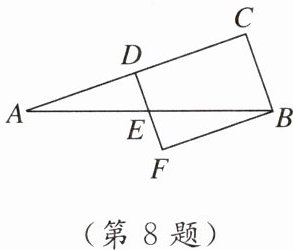
8. 如图,在Rt△ABC中,∠C= 90°,AC的垂直平分线分别交AC,AB于点D,E,过点B作DE的垂线,交DE的延长线于点F.已知DE= 1,AD= 3,则四边形BCDF的面积为
6
.
答案:
6 [点拨]由题意可知$∠C = ∠CDF = ∠F = 90^{\circ}$,
∴四边形BCDF是矩形,
∴$BF = DC$,又
∵$AD = DC$,
∴$BF = AD$,易证$△ADE≌△BFE$,
∴$DE = EF = 1$,
∴$DF = DE + EF = 1 + 1 = 2$。又
∵$DC = AD = 3$,
∴四边形BCDF的面积为$DC\cdot DF = 3×2 = 6$。
∴四边形BCDF是矩形,
∴$BF = DC$,又
∵$AD = DC$,
∴$BF = AD$,易证$△ADE≌△BFE$,
∴$DE = EF = 1$,
∴$DF = DE + EF = 1 + 1 = 2$。又
∵$DC = AD = 3$,
∴四边形BCDF的面积为$DC\cdot DF = 3×2 = 6$。
查看更多完整答案,请扫码查看


