《2025年综合应用创新题典中点九年级数学上册北师大版》

1. [2023常州期末]用一根长22cm的铁丝围成面积是$30cm^2$的矩形.假设矩形的一边长是xcm,则可列方程为 (B)
A. $ x(22 - x) = 30 $
B. $ x(11 - x) = 30 $
C. $ x(22 - 2x) = 30 $
D. $ 2x(22 - x) = 30 $

答案： B

2. (新考向 数学文化)我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则可列方程为 (A)
A. $ 3(x - 1)x = 6210 $
B. $ 3(x - 1) = 6210 $
C. $ (3x - 1)x = 6210 $
D. $ 3x = 6210 $

答案： A

3. (新考向 数学文化)我国古代著作《九章算术》“勾股”章有一题“今有户高多于广六尺八寸,两隅相去适一丈.问户高几何?”大意是说:已知长方形门的高比宽多6尺8寸,门的对角线长1丈(1丈= 10尺,1尺= 10寸),那么门的高为 (A)
A. 96寸
B. 86寸
C. 62寸
D. 28寸

答案： A

4. 如图,把小圆形场地的半径增加6m得到大圆形场地,场地面积扩大了一倍,则小圆形场地的半径为$(6+6\sqrt{2})$m.

答案： $(6+6\sqrt{2})$【点拨】设小圆形场地的半径为$r$m，则大圆形场地的半径为$(r+6)$m，由题意得，$\pi\times(r+6)^2=\pi\times r^2\times2$，解得$r_1=6+6\sqrt{2}$，$r_2=6-6\sqrt{2}＜0$（舍去）。
∴小圆形场地的半径为$(6+6\sqrt{2})$m。

5. 情境题·教育政策 2024·成都武侯区期末 《义务教育课程方案和课程标准(2022年版)》优化了课程内容结构,设立跨学科主题学习活动,以强化实践性要求,在一堂数学、美术的融合课中,每个同学桌上都有一段长60cm的铁丝,需要将铁丝剪成两段,并把每一段铁丝做成一个配件.
(1)填空:小东想做两个正方形配件,若设其中一个正方形配件的边长为xcm,则另一个正方形配件的边长为______(15-x)cm(请用含x的代数式表示).
(2)在(1)的基础上,若小东想让做成的两个正方形配件满足面积之和等于$100cm^2,$请问小东的想法能否实现?为什么?
小东的想法不能实现，理由如下：
假设小东的想法能实现，根据题意得：$x^2+(15-x)^2=100$，
整理，得$2x^2-30x+125=0$。
∵$\Delta=(-30)^2-4×2×125=-100＜0$，
∴原方程没有实数根。
∴假设不成立，即小东的想法不能实现。

答案： 【解】
(1)$(15-x)$
(2)小东的想法不能实现，理由如下：
假设小东的想法能实现，根据题意得：$x^2+(15-x)^2=100$，
整理，得$2x^2-30x+125=0$。
∵$\Delta=(-30)^2-4\times2\times125=-100＜0$，
∴原方程没有实数根。
∴假设不成立，即小东的想法不能实现。

6. 为响应国家“双减”政策,丰富学生的课余生活.“青青草原”社团打算规划一块面积为$300m^2$的土地,使它的长与宽的比为3:2,则宽约为多少米? (D)
A. 12m~13m之间
B. 13m~14m之间
C. 15m~16m之间
D. 14m~15m之间

答案： D

7. (新考向 知识情境化)如图,$ AB \perp OC $于点O,$ AO = BO = 50 \mathrm { cm } $,OC是射线,蚂蚁甲以2cm/s的速度从点A爬向点B,蚂蚁乙以3cm/s的速度从点O沿射线OC爬行,那么经过______s,两只蚂蚁和点O围成的三角形的面积为450cm^2.

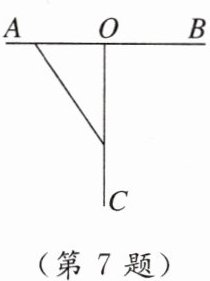
15 或 10 或 30

答案： 15 或 10 或 30【点拨】设经过$x$s，两只蚂蚁和点$O$围成的三角形的面积为$450cm^2$。①当$0\leq x\leq25$时，蚂蚁甲在线段$AO$上爬行，则由题意，得$\frac{1}{2}(50-2x)\cdot3x=450$。整理，得$x^2-25x+150=0$，解得$x_1=15$，$x_2=10$；②当$25＜x\leq50$时，蚂蚁甲在线段$OB$上爬行，则由题意，得$\frac{1}{2}(2x-50)\cdot3x=450$。整理，得$x^2-25x-150=0$，解得$x_1=30$，$x_2=-5$（不合题意，舍去）。综上所述，经过$15$s 或$10$s 或$30$s，两只蚂蚁和点$O$围成的三角形的面积为$450cm^2$。