第92页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
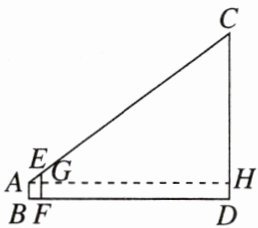
6. [2024德州陵城区期末]如图,线段AB,EF,CD分别表示人、竹竿、楼房的高度,且A,E,C在同一直线上,测得人和竹竿的水平距离为1.2m,人和楼房的水平距离为20m,人的高度为1.5m,竹竿的高度为3m,则楼房的高度是(
A. 25m
B. 26.5m
C. 50m
D. 51.5m
B
)
A. 25m
B. 26.5m
C. 50m
D. 51.5m
答案:
B [点拨]由题意知BF=AG=1.2m,BD=AH=20m,AB=FG=DH=1.5m,EF=3m,
∴EG=EF−FG=3−1.5=1.5(m).
易得EG//CH,
∴∠AGE=∠AHC,∠AEG=∠ACH.
∴△AEG∽△ACH.
∴$\frac{EG}{CH}$=$\frac{AG}{AH}$.
∴$\frac{1.5}{CH}$=$\frac{1.2}{20}$.
∴CH=25m.
∴CD=CH+DH=25+1.5=26.5(m).
故选B.
∴EG=EF−FG=3−1.5=1.5(m).
易得EG//CH,
∴∠AGE=∠AHC,∠AEG=∠ACH.
∴△AEG∽△ACH.
∴$\frac{EG}{CH}$=$\frac{AG}{AH}$.
∴$\frac{1.5}{CH}$=$\frac{1.2}{20}$.
∴CH=25m.
∴CD=CH+DH=25+1.5=26.5(m).
故选B.
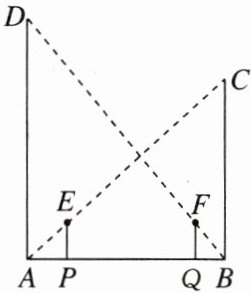
7. [2023济南市中区期末]如图所示,AD,BC为两路灯,身高相同的小明、小亮站在两路灯杆之间,两人相距6.5m,小明站在P处,小亮站在Q处,小明在路灯BC下的影长为2m,已知小明身高1.8m,路灯BC高9m.小明在路灯BC下的影子顶部恰好位于路灯DA的正下方,小亮在路灯AD下的影子顶部恰好位于路灯BC的正下方.
(1)计算小亮在路灯AD下的影长为
(2)计算路灯AD的高为
(1)计算小亮在路灯AD下的影长为
1.5m
;(2)计算路灯AD的高为
12m
.
答案:
[解]
(1)
∵EP⊥AB,CB⊥AB,
∴∠EPA=∠CBA=90°.
又
∵∠EAP=∠CAB,
∴△EAP∽△CAB.
∴$\frac{EP}{BC}$=$\frac{AP}{AB}$.
∴$\frac{1.8}{9}$=$\frac{2}{AB}$.
∴AB=10m.
∴BQ=10−2−6.5=1.5(m).
故小亮在路灯AD下的影长为1.5m.
(2)
∵FQ⊥AB,DA⊥AB,
∴∠FQB=∠DAB=90°.
又
∵∠FBQ=∠DBA,
∴△BFQ∽△BDA.
∴$\frac{FQ}{DA}$=$\frac{BQ}{AB}$.
∴$\frac{1.8}{DA}$=$\frac{1.5}{10}$.
∴DA=12m.
故路灯AD的高为12m.
(1)
∵EP⊥AB,CB⊥AB,
∴∠EPA=∠CBA=90°.
又
∵∠EAP=∠CAB,
∴△EAP∽△CAB.
∴$\frac{EP}{BC}$=$\frac{AP}{AB}$.
∴$\frac{1.8}{9}$=$\frac{2}{AB}$.
∴AB=10m.
∴BQ=10−2−6.5=1.5(m).
故小亮在路灯AD下的影长为1.5m.
(2)
∵FQ⊥AB,DA⊥AB,
∴∠FQB=∠DAB=90°.
又
∵∠FBQ=∠DBA,
∴△BFQ∽△BDA.
∴$\frac{FQ}{DA}$=$\frac{BQ}{AB}$.
∴$\frac{1.8}{DA}$=$\frac{1.5}{10}$.
∴DA=12m.
故路灯AD的高为12m.
8. 某数学“综合与实践”小组的同学把“测量学校旗杆的高度”作为一项课题活动,他们制订了测量方案,并利用课余时间完成了实地测量.测量方案与数据如表:
|课题|测量学校旗杆的高度|
|----|----|
|测量工具|皮尺、标杆等|
|测量方案示意图| |
|
|说明|A,E,C三点共线,D,F,B三点共线,CD,EF,AB均垂直于AC|
|测量数据|标杆EF= 2.05m,小明的身高CD= 1.65m,CE= 1m,AE= 21m|
请根据方案及其数据求出学校旗杆的高度AB.
|课题|测量学校旗杆的高度|
|----|----|
|测量工具|皮尺、标杆等|
|测量方案示意图|
 |
||说明|A,E,C三点共线,D,F,B三点共线,CD,EF,AB均垂直于AC|
|测量数据|标杆EF= 2.05m,小明的身高CD= 1.65m,CE= 1m,AE= 21m|
请根据方案及其数据求出学校旗杆的高度AB.
答案:
[解]如图,过D作DM⊥AB于M,交EF于N.
又
∵DC⊥AC,FE⊥AC,AB⊥AC,
∴EF//AB,易得四边形CDNE,四边形AMNE是矩形.
∴DN=CE=1m,MN=AE=21m,
NE=AM=CD=1.65m.
∴FN=FE−EN=2.05−1.65=0.4(m),DM=DN+MN=1+21=22(m).
∵FN//BM,
∴∠FND=∠BMD,∠NFD=∠MBD.
∴△DFN∽△DBM.
∴FN:BM=DN:DM.
∴0.4:BM=1:22.
∴MB=8.8m.
∴AB=AM+MB=8.8+1.65=10.45(m).
故学校旗杆的高度AB是10.45m.

[解]如图,过D作DM⊥AB于M,交EF于N.
又
∵DC⊥AC,FE⊥AC,AB⊥AC,
∴EF//AB,易得四边形CDNE,四边形AMNE是矩形.
∴DN=CE=1m,MN=AE=21m,
NE=AM=CD=1.65m.
∴FN=FE−EN=2.05−1.65=0.4(m),DM=DN+MN=1+21=22(m).
∵FN//BM,
∴∠FND=∠BMD,∠NFD=∠MBD.
∴△DFN∽△DBM.
∴FN:BM=DN:DM.
∴0.4:BM=1:22.
∴MB=8.8m.
∴AB=AM+MB=8.8+1.65=10.45(m).
故学校旗杆的高度AB是10.45m.

查看更多完整答案,请扫码查看


