《2025年综合应用创新题典中点九年级数学上册北师大版》

9. 母题·教材P19习题T5 “出入相补”原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形ABCD中,$AB= 5$,$AD= 12$,对角线AC与BD交于点O,点E为BC边上的一个动点,$EF⊥AC,EG⊥BD$,垂足分别为点F,G,则$EF+EG=$$\frac{60}{13}$.

答案： $\frac{60}{13}$ 【点拨】连接 $OE$。
$\because$ 四边形 $ABCD$ 是矩形，
$\therefore \angle ABC = 90^{\circ}$，$BC = AD = 12$，$OA = OC = \frac{1}{2}AC$，$OB = OD = \frac{1}{2}BD$，$AC = BD$。
又 $\because AB = 5$，$\therefore AC = \sqrt{AB^{2} + BC^{2}} = 13$。
$\therefore OC = \frac{1}{2}AC = \frac{13}{2}$，$OB = \frac{1}{2}BD = \frac{1}{2}AC = \frac{13}{2}$。
又 $\because S_{\triangle BOC} = S_{\triangle BOE} + S_{\triangle COE} = \frac{1}{2}OB \cdot EG + \frac{1}{2}OC \cdot EF = \frac{1}{2}S_{\triangle ABC} = \frac{1}{2} \times \frac{1}{2} \times 5 \times 12 = 15$，
$\therefore \frac{1}{2} \times \frac{13}{2}EG + \frac{1}{2} \times \frac{13}{2}EF = \frac{1}{2} \times \frac{13}{2}(EG + EF) = 15$。
$\therefore EG + EF = \frac{60}{13}$。

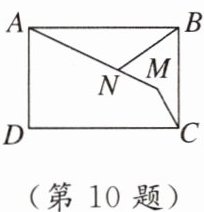
10. 2024·深圳福田区模拟 如图,点M是矩形ABCD内一个动点,$AB= AM= 6,BC= 4$,点N为线段AM上一点,且$AN= \frac {2}{3}AM$,连接BN和CM,则$BN+CM$的最小值为$2\sqrt{5}$.

答案： $2\sqrt{5}$ 【点拨】在 $AB$ 上截取 $BE = MN$，连接 $ME$，$CE$。
$\because AN = \frac{2}{3}AM$，$AB = AM = 6$，$\therefore AN = 4$，$MN = 2$。
$\therefore BE = MN = 2$。
$\therefore AE = AB - BE = 6 - 2 = 4$。$\therefore AE = AN$。
又 $\because AB = AM$，$\angle BAN = \angle MAE$，
$\therefore \triangle BAN \cong \triangle MAE(SAS)$。
$\therefore BN = ME$。
$\therefore BN + CM = ME + CM \geq CE$。
$\therefore$ 当 $C$，$M$，$E$ 在一条直线上时，$ME + CM$ 最小，最小值为 $CE$ 的长。
$\because$ 四边形 $ABCD$ 是矩形，
$\therefore \angle ABC = 90^{\circ}$。
在 $Rt\triangle BCE$ 中，$BC = 4$，$BE = 2$，
$\therefore CE = \sqrt{BC^{2} + BE^{2}} = \sqrt{4^{2} + 2^{2}} = 2\sqrt{5}$。
即 $BN + CM$ 的最小值为 $2\sqrt{5}$。

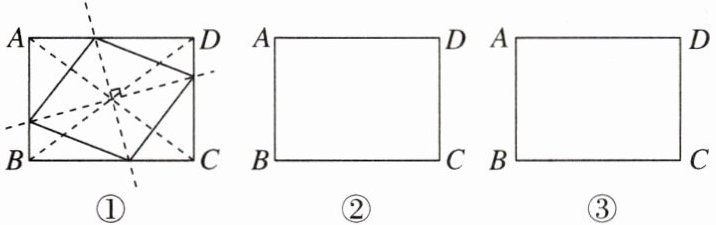
11. 情境题·兴趣活动型 某校数学兴趣小组用一张矩形纸片剪出一张菱形纸片,要求菱形的各个顶点均落在矩形的边或顶点上,如图①,过矩形两对角线的交点,作两条互相垂直的直线与矩形四边相交,依次连接四个交点,沿连线可剪出菱形.
(1)请在图②,图③中画出两种符合要求的示意图;
(2)若$AB= 6cm,BC= 8cm$,从(1)中选择一种示意图,求出你所作的菱形的边长.

答案：

(1)【解】符合要求的示意图如图所示。(答案不唯一)
　　　　 　　　
(2)选择如图①所示的示意图。
菱形边长 $AB = 6cm$。
选择如图②所示的示意图。
由 $AB = 6cm$，$BC = 8cm$，
易得菱形边长 $EF = \sqrt{(6 \div 2)^{2} + (8 \div 2)^{2}} = 5(cm)$。

12. [2024广州越秀区模拟] 如图①,已知锐角三角形ABC中,CD,BE分别是AB,AC边上的高,M,N分别是线段BC,DE的中点,连接DM,ME,MN.
(1)求证:$MN⊥DE$.
(2)猜想$∠A与∠DME$之间的关系,并证明猜想.
猜想：$\angle DME=180^{\circ}-2\angle A$
(3)当$∠A$变为钝角时,如图②,上述(1)(2)中的结论是否都成立,若结论成立,直接回答,不需证明;若结论不成立,说明理由.
结论：结论(1)成立，结论(2)不成立

答案：
(1)【证明】$\because CD$，$BE$ 分别是 $AB$，$AC$ 边上的高，$M$ 是 $BC$ 的中点，
$\therefore DM = \frac{1}{2}BC$，$ME = \frac{1}{2}BC$，
$\therefore DM = ME$。
又 $\because N$ 为 $DE$ 的中点，$\therefore MN \perp DE$。
(2)【解】$\angle DME = 180^{\circ} - 2\angle A$。
证明：在 $\triangle ABC$ 中，$\angle ABC + \angle ACB = 180^{\circ} - \angle A$。
由
(1)易知 $DM = ME = BM = MC$，
$\therefore \angle ABC = \angle MDB$，$\angle ACB = \angle MEC$。
$\therefore \angle BMD + \angle CME = (180^{\circ} - 2\angle ABC) + (180^{\circ} - 2\angle ACB) = 360^{\circ} - 2(\angle ABC + \angle ACB) = 360^{\circ} - 2(180^{\circ} - \angle A) = 2\angle A$。
$\therefore \angle DME = 180^{\circ} - (\angle BMD + \angle CME) = 180^{\circ} - 2\angle A$。
(3)【解】结论
(1)成立，结论
(2)不成立。
理由如下：在 $\triangle ABC$ 中，$\angle ABC + \angle ACB = 180^{\circ} - \angle BAC$。
易知 $DM = ME = BM = MC$，
$\therefore \angle MBD = \angle MDB$，$\angle MEC = \angle MCE$。
$\therefore \angle DME = \angle BMD + \angle EMC - 180^{\circ} = (180^{\circ} - 2\angle MBD) + (180^{\circ} - 2\angle MCE) - 180^{\circ} = 2[180^{\circ} - (\angle MBD + \angle MCE)] - 180^{\circ} = 2[180^{\circ} - (180^{\circ} - \angle BAC)] - 180^{\circ} = 2\angle BAC - 180^{\circ}$。

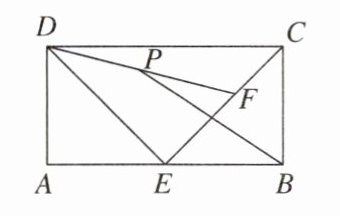
13. 新视角 动点探究题 如图,矩形ABCD中,$AB= 4$,$AD= 2$,E为AB的中点,F为EC上一动点,P为DF的中点,连接PB,则PB的最小值是____.

答案：
$2\sqrt{2}$ 【点拨】如图，取 $CD$ 和 $DE$ 的中点 $P_{1}$，$P_{2}$，连接 $BP_{1}$，$P_{1}P_{2}$，$P_{1}P$。
　　　　　　　　　
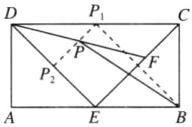
当点 $F$ 与点 $C$ 重合时，点 $P$ 在 $P_{1}$ 处。
当点 $F$ 与点 $E$ 重合时，点 $P$ 在 $P_{2}$ 处。
易知 $P_{1}P_{2} // CE$ 且 $P_{1}P_{2} = \frac{1}{2}CE$。
当点 $F$ 在 $EC$ 上除点 $C$，$E$ 的位置外时，有 $DP = FP$。
由中位线定理可知，$P_{1}P // CE$ 且 $P_{1}P = \frac{1}{2}CF$。
$\therefore$ 点 $P$ 的运动轨迹是线段 $P_{1}P_{2}$。
$\therefore$ 当 $BP \perp P_{1}P_{2}$ 时，$PB$ 取得最小值。
$\because$ 在矩形 $ABCD$ 中，$AB = 4$，$AD = 2$，$E$ 为 $AB$ 的中点，
$\therefore \triangle CBE$，$\triangle ADE$，$\triangle BCP_{1}$ 为等腰直角三角形，$CP_{1} = 2$。
$\therefore \angle ADE = \angle AED = \angle BEC = \angle CP_{1}B = 45^{\circ}$。
$\therefore \angle DEC = 90^{\circ}$，$\angle EDC = 45^{\circ}$。
又 $\because P_{1}P_{2} // CE$，
$\therefore \angle DP_{2}P_{1} = \angle DEC = 90^{\circ}$，$\therefore \angle DP_{1}P_{2} = 45^{\circ}$。
$\therefore \angle P_{2}P_{1}B = 90^{\circ}$，即 $BP_{1} \perp P_{1}P_{2}$。
$\therefore BP$ 的最小值为 $BP_{1}$ 的长。
在等腰直角三角形 $BCP_{1}$ 中，$CP_{1} = BC = 2$，$\therefore BP_{1} = 2\sqrt{2}$。
$\therefore PB$ 的最小值是 $2\sqrt{2}$。