《2025年综合应用创新题典中点九年级数学上册北师大版》

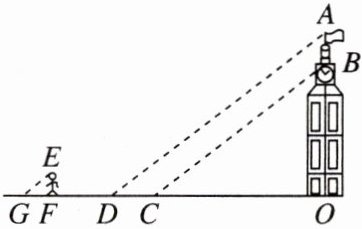
14. 小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高．如图所示,在某一时刻,他们在阳光下,分别测得该建筑物$OB的影长OC为16\mathrm{m}$,$OA的影长OD为20\mathrm{m}$,小明的影长$FG为2.4\mathrm{m}$,其中$O$,$C$,$D$,$F$,$G$五点在同一直线上,$A$,$B$,$O$三点在同一直线上,且$AO\perp OD$,$EF\perp FG$．已知小明的身高$EF为1.8\mathrm{m}$,求旗杆的高$AB$．

[解]∵AD//EG,
　　∴∠ADO = ∠EGF.
　　∵AO⊥OD,EF⊥FG,∴∠AOD = ∠EFG = 90°.
　　∴△AOD∽△EFG
　　∴$\frac{AO}{EF}$ = $\frac{OD}{FG}$,即$\frac{AO}{1.8}$ = $\frac{20}{2.4}$.
　　∴AO = 15米.
　　∵AD//BC,
　　∴∠BCO = ∠ADO,∠DAO = ∠CBO.
　　∴△BOC∽△AOD.
　　∴$\frac{BO}{AO}$ = $\frac{OC}{OD}$,即$\frac{BO}{15}$ = $\frac{16}{20}$.
　　∴BO = 12米.
　　∴AB = AO - BO = 15 - 12 = 3(米).
　　∴旗杆的高AB是3米.

答案： [解]
∵AD//EG,
　
∴∠ADO = ∠EGF.
　
∵AO⊥OD,EF⊥FG,
∴∠AOD = ∠EFG = 90°.
　
∴△AOD∽△EFG
　
∴$\frac{AO}{EF}$ = $\frac{OD}{FG}$,即$\frac{AO}{1.8}$ = $\frac{20}{2.4}$.
　
∴AO = 15米.
　
∵AD//BC,
　
∴∠BCO = ∠ADO,∠DAO = ∠CBO.
　
∴△BOC∽△AOD.
　
∴$\frac{BO}{AO}$ = $\frac{OC}{OD}$,即$\frac{BO}{15}$ = $\frac{16}{20}$.
　
∴BO = 12米.
　
∴AB = AO - BO = 15 - 12 = 3(米).
　
∴旗杆的高AB是3米.

15. [2023遂宁]在方格图中,以格点为顶点的三角形叫做格点三角形．在如图所示的平面直角坐标系中,格点$\triangle ABC$,$\triangle DEF$成位似关系,则位似中心的坐标为(A)

A. $(-1,0)$
B. $(0,0)$
C. $(0,1)$
D. $(1,0)$

答案： A

16. 如图,$\triangle ABO的顶点坐标是A(2,6)$,$B(3,1)$,$O(0,0)$,以点$O$为位似中心,将$\triangle ABO缩小为原来的\frac {1}{3}$,得到$\triangle A'B'O$,则点$A'$的坐标为$(\frac{2}{3},2)$ 或 $(-\frac{2}{3},-2)$．

答案： $(\frac{2}{3},2)$ 或 $(-\frac{2}{3},-2)$ [点拨]
∵以原点O为位似中心, 把△ABO缩小为原来的$\frac{1}{3}$, 可以得到△$A'B'O$, 点A的坐标为(2,6),
∴点$A'$的坐标是$(2×\frac{1}{3},6×\frac{1}{3})$ 或$(2×(-\frac{1}{3}),6×(-\frac{1}{3}))$, 即$(\frac{2}{3},2)$ 或$(-\frac{2}{3},-2)$.

17. 如图,$A$,$B$,$O$三点都在方格纸的格点上,请按要求在方格纸内作图．
(1)在图①中以点$O$为位似中心,作线段$AB的位似图形CD$,使其长度为$AB$的2倍．
(2)已知$\triangle OPQ的三边比为1:2:\sqrt {5}$,在图②中画格点$\triangle ABD$,使$\triangle ABD与\triangle OPQ$相似．

答案：
[解]
(1)如图①,线段CD即为所求. (答案不唯一)
(2)如图②,△ABD即为所求(答案不唯一).