第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
11. 新视角·动点探究题 [2024·无锡惠山区期中]如图,在矩形ABCD中,$AB= 5$,$BC= 4$,动点P从点B出发,以每秒2个单位长度的速度,沿射线BC方向运动,动点Q从点C出发,以每秒1个单位长度的速度,沿线段CD方向运动.点P和点Q同时出发,当点Q到达点D时,两点同时停止运动,设运动时间为$ts(t>0)$.
(1)用含t的代数式表示线段CP的长;
(2)当PQ与矩形的对角线平行时,求t的值,

(1)用含t的代数式表示线段CP的长;
(2)当PQ与矩形的对角线平行时,求t的值,

答案:
[解]
(1)
∵四边形ABCD为矩形,AB = 5,BC = 4,
∴CD = AB = 5,AD = BC = 4,AD // BC.
∵点Q在CD上运动,运动的速度为每秒1个单位长度,且点Q到达点D时停止运动,
∴点Q从点C运动到点D所用的时间为 $5 \div 1 = 5$ (秒),且CQ = t.
∴0 < t ≤ 5.
∵动点P从点B出发,以每秒2个单位长度的速度,运动时间为t秒 (t > 0),
∴BP = 2t.
① 当0 < t ≤ 2时,CP = 4 - 2t;
② 当2 < t ≤ 5时,CP = 2t - 4.
(2)当PQ与矩形ABCD的对角平行时,有以下两种情况:①当PQ // BD时,此时点P在线段BC上,如图①,

则0 < t ≤ 2.
[解]
(1)
∵四边形ABCD为矩形,AB = 5,BC = 4,
∴CD = AB = 5,AD = BC = 4,AD // BC.
∵点Q在CD上运动,运动的速度为每秒1个单位长度,且点Q到达点D时停止运动,
∴点Q从点C运动到点D所用的时间为 $5 \div 1 = 5$ (秒),且CQ = t.
∴0 < t ≤ 5.
∵动点P从点B出发,以每秒2个单位长度的速度,运动时间为t秒 (t > 0),
∴BP = 2t.
① 当0 < t ≤ 2时,CP = 4 - 2t;
② 当2 < t ≤ 5时,CP = 2t - 4.
(2)当PQ与矩形ABCD的对角平行时,有以下两种情况:①当PQ // BD时,此时点P在线段BC上,如图①,

则0 < t ≤ 2.
12. 【教材呈现】下面是北师版教材九年级上册82页的部分内容:
一般地,有如下基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
【问题原型】如图①,在矩形ABCD中,点E为边AB的中点,过点E作$EF// AD$交边DC于点F,点P,Q分别在矩形的边AD,BC上,连接PQ交EF于点M.求证:$PM= QM$.
【结论应用】在【问题原型】的基础上,点R在边BC上(不与点Q重合),连接PR交EF于点N.
(1)如图②,若$MN= 4$,则线段QR的长为______;
(2)当点Q与点B重合,点R与点C重合时,如图③,若$BC= 10$,且$\triangle PMN$周长的最小值为12,则边AB的长为______.
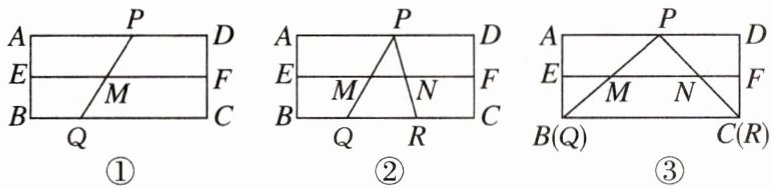
一般地,有如下基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
【问题原型】如图①,在矩形ABCD中,点E为边AB的中点,过点E作$EF// AD$交边DC于点F,点P,Q分别在矩形的边AD,BC上,连接PQ交EF于点M.求证:$PM= QM$.
【结论应用】在【问题原型】的基础上,点R在边BC上(不与点Q重合),连接PR交EF于点N.
(1)如图②,若$MN= 4$,则线段QR的长为______;
(2)当点Q与点B重合,点R与点C重合时,如图③,若$BC= 10$,且$\triangle PMN$周长的最小值为12,则边AB的长为______.

答案:
(1)解:
因为,。
根据“两条直线被一组平行线所截,所得的对应线段成比例”,在中,(已证),。
所以是中点,是中点。
则是的中位线。
根据三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半,即。
已知,所以。
(2)
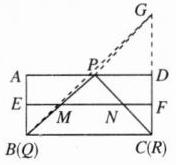
(2)$2\sqrt{6}$【点拨】如图所示,作点$C$关于$AD$的对称点$G$,连接$PG$,$BG$,$\therefore PG = PC$.$\therefore PB + PC = PB + PG\geqslant BG$.
∴当点 $ P $ 在 $ BG $ 上时,$ PB + PC $ 取得最小值。
又 $ \because PD // BC $,$ D $ 是 $ CG $ 的中点,$ \therefore $ 点 $ P $ 是 $ BG $ 的中点。
$ \therefore PB = PG = PC $,易证 $ P $ 是 $ AD $ 的中点。
即当 $ P $ 是 $ AD $ 的中点时,$ \triangle PBC $ 的周长取得最小值。
根据(1)的结论得出 $ MN $ 是 $ \triangle PQR $ 的中位线。
又 $ \because BC = 10 $,且 $ \triangle PMN $ 周长的最小值为 $ 12 $,
$ \therefore PA = PD = \frac{1}{2}AD = \frac{1}{2}BC = 5 $,易得 $ \triangle PBC $ 的周长为 $ 24 $。
$ \therefore PB + PC = 24 - 10 = 14 $。
$ \therefore PB = 7 $。
$ \therefore AB = \sqrt{PB^{2} - AP^{2}} = \sqrt{7^{2} - 5^{2}} = 2\sqrt{6} $。
(1)解:
因为,。
根据“两条直线被一组平行线所截,所得的对应线段成比例”,在中,(已证),。
所以是中点,是中点。
则是的中位线。
根据三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半,即。
已知,所以。
(2)
(2)$2\sqrt{6}$【点拨】如图所示,作点$C$关于$AD$的对称点$G$,连接$PG$,$BG$,$\therefore PG = PC$.$\therefore PB + PC = PB + PG\geqslant BG$.
∴当点 $ P $ 在 $ BG $ 上时,$ PB + PC $ 取得最小值。
又 $ \because PD // BC $,$ D $ 是 $ CG $ 的中点,$ \therefore $ 点 $ P $ 是 $ BG $ 的中点。
$ \therefore PB = PG = PC $,易证 $ P $ 是 $ AD $ 的中点。
即当 $ P $ 是 $ AD $ 的中点时,$ \triangle PBC $ 的周长取得最小值。
根据(1)的结论得出 $ MN $ 是 $ \triangle PQR $ 的中位线。
又 $ \because BC = 10 $,且 $ \triangle PMN $ 周长的最小值为 $ 12 $,
$ \therefore PA = PD = \frac{1}{2}AD = \frac{1}{2}BC = 5 $,易得 $ \triangle PBC $ 的周长为 $ 24 $。
$ \therefore PB + PC = 24 - 10 = 14 $。
$ \therefore PB = 7 $。
$ \therefore AB = \sqrt{PB^{2} - AP^{2}} = \sqrt{7^{2} - 5^{2}} = 2\sqrt{6} $。

查看更多完整答案,请扫码查看


