《2025年综合应用创新题典中点九年级数学上册北师大版》

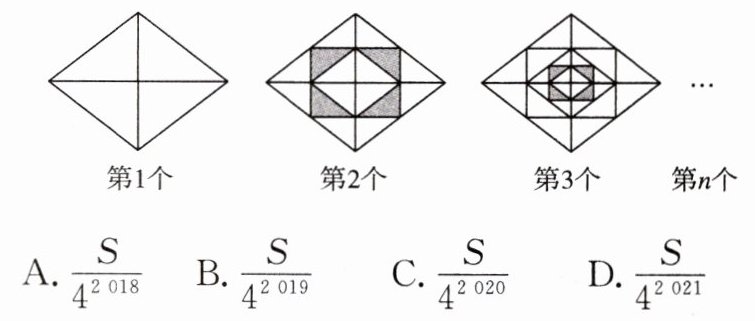
10. 学科素养 逻辑推理 如图,在一组由菱形和矩形组成的图案中,第1个图中菱形的面积为S(S为常数),第2个图中阴影部分是由连接菱形各边中点得到的矩形和再连接矩形各边中点得到的菱形产生的,…,以此类推,则第2020个图中阴影部分的面积可以用含S的代数式(S≥2且S是正整数)表示为($\frac{S}{4^{2019}}$)

答案： B [点拨]观察题图发现：
第2个图形中的阴影部分的面积为$\frac{S}{4}$，
第3个图形中的阴影部分的面积为$\frac{S}{16}$，
…
第n个图形中的阴影部分的面积为$\frac{S}{4^{n - 1}}$.
故第2020个图中阴影部分的面积可以用含S的代数式表示为$\frac{S}{4^{2019}}$.

11. 如图,四边形ABCD的对角线AC,BD交于点O,点M,N,P,Q分别为边AB,BC,CD,DA的中点.有下列四个推断：

①对于任意四边形ABCD,四边形MNPQ可能不是平行四边形；
②若AC= BD,则四边形MNPQ一定是菱形；
③若AC⊥BD,则四边形MNPQ一定是矩形；
④若四边形ABCD是菱形,则四边形MNPQ也是菱形.
其中正确的序号是______②③.

答案： ②③

12. 新考法 阅读类比法 阅读下面材料：
在数学课上,老师请同学们思考如下问题：如图①,我们把一个四边形ABCD的各边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗？
小敏在思考问题时,有如下思路：连接AC.

结合小敏的思路作答.
(1)若只改变图①中四边形ABCD的形状(如图②),则四边形EFGH还是平行四边形吗？说明理由.
(2)如图②,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明.
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

答案：
[解]
(1)四边形EFGH是平行四边形.
理由:如图，连接AC,
∵E是AB的中点，F是BC的中点，
∴EF//AC，$EF = \frac{1}{2}AC$.
同理HG//AC，$HG = \frac{1}{2}AC$.
∴EF//HG，EF=HG.
∴四边形EFGH是平行四边形.
(2)①当AC=BD时，四边形EFGH是菱形. 证明如下：
由
(1)知，四边形EFGH是平行四边形，$HG = \frac{1}{2}AC$，且易知$FG = \frac{1}{2}BD$.
∵AC=BD，
∴FG=HG.
∴平行四边形EFGH是菱形.
②当AC⊥BD时，四边形EFGH是矩形.