《2025年综合应用创新题典中点九年级数学上册北师大版》

9. [2023聊城]在一个不透明的袋子中,装有五个分别标有数字$-\sqrt {3},\sqrt {6},0,2,π$的小球,这些小球除数字外其他完全相同.从袋子中随机摸出两个小球,两球上的数字之积恰好是有理数的概率为____.

答案：
$\frac{2}{5}$ [点拨]画树状图如图:
由树状图可知，共有20种等可能的结果，其中两球上的数字之积恰好是有理数的结果有8种，
∴两球上的数字之积恰好是有理数的概率为$\frac{8}{20}=\frac{2}{5}$.

10. [2024武汉洪山区模拟]我们去游泳馆游泳时,要换拖鞋,如果大桶里只剩下尺码相同的2双红色拖鞋和1双蓝色拖鞋混放在一起,闭上眼睛随意拿出2只,它们恰好是一双的概率是____.

答案：
$\frac{1}{3}$ [点拨]设两双红色拖鞋分别是a,A,a,A;1双蓝色拖鞋是c,C,列表如下:
　　　　　　
　由表可知，共有30种等可能的结果，其中它们恰好是一双的结果有10种，所以它们恰好是一双的概率是$\frac{10}{30}=\frac{1}{3}$.

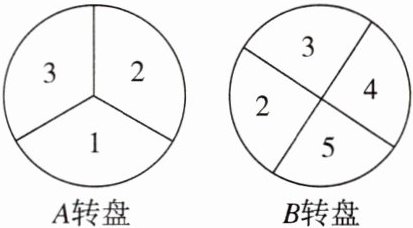
11. 母题 教材P73复习题T8 小明和小亮都想参加“象棋”社团活动,但受到名额限制,只能录取一人,他们用如图所示的A,B两个转盘(每个转盘被平均分成面积相等的扇形)做游戏:同时转动两个转盘,若两次数字之差的绝对值为奇数,则小明胜;若两次数字之差的绝对值为偶数,则小亮胜.这个游戏对双方公平吗?请你用列表或画树状图的方法说明理由.

答案：
[解]这个游戏对双方公平，理由如下:
　画树状图如图:
　　　　
　　由树状图可知，共有12种等可能的结果，其中两次数字之差的绝对值为奇数的结果有6种，两次数字之差的绝对值为偶数的结果有6种，
　
∴小明胜的概率为$\frac{6}{12}=\frac{1}{2}$,小亮胜的概率为$\frac{6}{12}=\frac{1}{2}$.
∴小明胜的概率=小亮胜的概率.
　
∴这个游戏对双方公平

12. 新趋势 跨学科 田忌赛马的故事为我们熟知,在学习概率知识后老师设计了如下游戏:已知甲、乙两人手中各有牌面数字为2,5,7和3,6,8的三张扑克牌,每次同时各出一张牌(打出的牌不收回),谁的牌数字大谁赢.
(1)若甲、乙将手中的牌随机抽出一张,一局定胜负,请用列表或画树状图的方法,比较谁获胜的机会大?
(2)若规定三局两胜者为胜,已知乙按从小到大的顺序出牌,则甲应该怎样出牌,才能保证获胜?

答案：
[解]
(1)画树状图如图:
　　　　　　　
　　由树状图可知，共有9种等可能的结果，其中甲获胜的结果有3种，乙获胜的结果有6种，
　
∴甲获胜的概率是$\frac{3}{9}=\frac{1}{3}$,乙获胜的概率为$\frac{6}{9}=\frac{2}{3}$.
∵$\frac{1}{3}$＜$\frac{2}{3}$,
　
∴乙获胜的机会大,
(2)由题意得，乙出牌的顺序为(3,6,8)，甲随机出牌的顺序有(2,5,7),(2,7,5),(5,2,7),(5,7,2),(7,2,5),(7,5,2),
　易知当甲按(5,7,2)的顺序出牌时，才能保证获胜.